Ogni corpo dotato di massa esercita sugli altri corpi una forza di tipo attrattivo, che viene detta "attrazione gravitazionale". Essa è proporzionale al prodotto delle masse dei due corpi e decresce con il quadrato della loro distanza. Inoltre è reciproca: i due corpi si attraggono simultaneamente con la stessa intensità.
Il campo gravitazionale di un corpo è la regione dello spazio
all'interno della quale si esercita l'attrazione gravitazionale di quel
corpo.
Si tratta in sostanza di un valore numerico che indica l'intensità
(o grandezza) dell'influenza gravitazionale di quel corpo in ogni punto
dello spazio. Quando un altro corpo si trova in quel punto, viene attratto
verso il primo con una forza tanto maggiore quanto maggiori sono la propria
massa e il valore del campo gravitazionale in quel punto.
A rigore il campo gravitazionale di un corpo qualsiasi si estende nell'intero Universo, ma in pratica l'attrazione che esso esercita rimane significativa solo nelle sue immediate vicinanze (anche se nel caso di un quasar o di una galassia le "immediate vicinanze" possono estendersi su milioni di anni luce).
La teoria della relatività di Einstein prevede addirittura che
possano esistere corpi celesti dotati di un campo gravitazionale talmente
intenso che neppure la radiazione elettromagnetica possa sottrarsi alle
forze attrattive che si manifestano all'interno di esso, arrivando alla
definizione di corpo nero, in tale caso limite possiamo immaginare l'esistenza
di una superficie sferica limite,detta orizzonte degli eventi, attraverso
la quale la luce può entrare, ma non riesce più ad uscire.
Un buco nero deve essere o un corpo di densità elevatissima, avente una massa relativamente piccola, come quella del Sole o anche minore, compressa in un volume estremamente ridotto (una mela);oppure un corpo di bassa densità ma di massa enorme, pari a milioni di volte la massa del Sole, posto nel centro di una galassia.
Escludendo i casi limite è possibile determinare le caratteristiche del campo gravitazionale partendo dalla legge di gravitazione universale di Newton.
Il vettore del campo
Secondo la legge di gravitazione di Newton, il modulo della forza gravitazionale esercitata su una massa M2 da una massa m, situata a una distanza r dalla prima è
Si sa che F è una grandezza vettoriale e che la forza
agente su M2 è diretta verso M1
Invece di scrivere una legge della forza per il caso di una particolare massa M2, dividiamo entrambi i membri dell'equazione per M2: il secondo membro di questa espressione dipende ora solo dalla distanza di M2 da M1, e non dalla massa di M2. Cioè, il secondo membro è una descrizione del campo gravitazionale a questa distanza dovuto alla massa-sorgente e resterà immutato qualunque sia la massa M2 collocata in questa posizione. Perciò, riscriviamo questa espressione in una forma che mette in evidenza solo la massa- sorgente. La nuova grandezza, che è il secondo membro dell'equazione precedente e che descrive il campo gravitazionale di m1, sarà denotata con g:
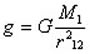
dove la massa-sorgente M1 è ora indicata con M. Le dimensioni di g sono quelle di una forza divisa per una massa, ossia di un'accelerazione.
Poiché la forza gravitazionale Fgrav è un vettore, la grandezza g è anch'essa un vettore. La descrizione completa del campo gravitazionale (modulo e orientazione) dovuto alla massa-sorgente M in un punto qualsiasi P è data da g, il vettore campo gravitazionale.
Il vettore del campo, g, dà la forza per unità di massa agente su (o l'accelerazione di) un oggetto qualsiasi collocato nel campo gravitazionale della massa-sorgente M. La forza gravitazionale che agisce sulla massa m è
| Fgrav =mg |
Questa equazione è esattamente il corrispondente vettoriale della familiare equazione scalare, F=mg, che abbiamo usato in precedenza per calcolare le forze gravitazionali. In realtà, l'accelerazione dovuta alla gravità, g, che abbiamo usato, è semplicemente il modulo del vettore del campo, g. Naturalmente, il vettore del campo, g, è una grandezza più generale e varia con la posizione nello spazio, ma sulla superficie della Terra ha come modulo 9,81 m/sec2.
Il principio di sovrapposizione
Uno dei fatti che rendono così utile il concetto di campo nel caso gravitazionale (come pure nel caso elettrico, come vedremo) è che il vettore forza gravitazionale e il vettore campo gravitazionale ubbidiscono al principio di sovrapposizione. Cioè, se si vuole calcolare la forza esercitata su un dato oggetto da molti altri oggetti, la forza risultante è la somma vettoriale di tutte le forze individuali; ciascuna di queste forze individuali può essere calcolata come se gli altri oggetti non fossero presenti. Perciò,
| Fgrav = F1 + F2 + F3 +… |
Poiché il vettore campo gravitazionale è semplicemente la forza per unità di massa, ne consegue che g ubbidisce ad una analoga relazione additiva:
| gris= g1+g2+g3+ … |
Dire che la forza gravitazionale che
agisce su un oggetto è la somma vettoriale di tutte le forze contribuenti,
ciascuna calcolata senza tener conto delle altre, non è un'asserzione
insignificante o banale. Per esempio, consideriamo la forza che agisce
su una massa m per effetto di altre due masse, Mi ed M2.
Il principio di sovrapposizione dice che la forza agente su m è Il fatto
che M2 giaccia fra Mi ed m non influenza il calcolo
della forza dovuta a Mi. Cioè, M2 non «scherma»
od «oscura» la forza esercitata da Mi su m: è la stessa, sia
presente o no M2. Questo risultato è ottenuto solo per via
sperimentale. In primo luogo, si ipotizza il principio di sovrapposizione
e se ne traggono le conseguenze. (Per esempio, non è solo la superficie
della Terra che attrae la Luna, è l'intera massa della Terra che agisce,
e ciascuna piccola porzione svolge la sua funzione indipendentemente dalle
altre porzioni.) In secondo luogo, queste conseguenze sono verificate
per confronto con i risultati sperimentali. Poiché non è mai stata riscontrata
alcuna contraddizione, il principio di sovrapposizione per le forze gravitazionali
è considerato valido.
