La spiegazione di questo effetto fornisce una definitiva conferma del concetto
di fotone come quanto di energia. La dimostrazione della spiegazione fu data
nel 1923 da Arthur Holly Compton (1892-1962) che per questo suo lavoro nel
1927 ottenne il premio Nobel per la fisica.
Realizzazione sperimentale
Compton inviò un fascio monocromatico di raggi X di lunghezza d'onda
l su un blocco di grafite e misurò, per
vari angoli di diffusione, l'intensità dei raggi X in funzione della
lunghezza d'onda.
Per quanto il fascio incidente abbia una sola lunghezza d'onda l,
i raggi X diffusi hanno picchi d'intensità a due lunghezza d'onda;
uno di essi corrisponde alla lunghezza d'onda incidente, l'altro alla lunghezza
d'onda l' che è superiore alla precedente
della quantità Dl. Questo Dl,
chiamato spostamento Compton, varia col variare dell'angolo a cui sono
osservati i raggi X diffusi.
|
|
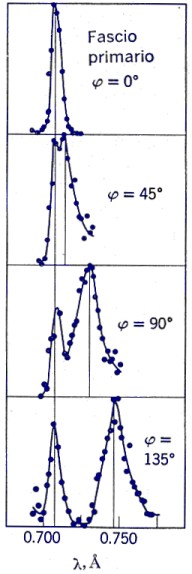
| Risultati sperimentali di Compton. La linea verticale a sinistra corrisponde alla lunghezza d'onda l, quella a destra a l'. Vengono mostrati i risultati per quattro diversi angoli di diffusione j. Notare che lo spostamento Compton Dl per j=90° è di h/m0c=0,242 Å. [da: D. Halliday, R. Resnick, op. cit.] |
|
Discussione dell'effetto osservato
La presenza di un'onda diffusa di lunghezza d'onda l'
non può essere spiegata se i raggi X incidenti sono considerati come
un'onda elettromagnetica. In questo caso, infatti, l'onda incidente, di frequenza
n, fa sì che gli elettroni del blocco su
cui avviene la diffusione, oscillino alla stessa frequenza. Questi elettroni
oscillanti, paragonabili alle cariche che si muovono avanti ed indietro in
una minuscola radioantenna, irradiano onde elettromagnetiche della stessa
frequenza n. Quindi nella descrizione ondulatoria
l'onda diffusa dovrebbe avere le stessa frequenza e lunghezza d'onda dell'onda
incidente.
Compton fu in grado di spiegare i risultati sperimentali da lui ottenuti postulando
che il fascio di raggi X incidente non fosse un'onda, ma un insieme di fotoni
di energia E=hn e che questi urtassero gli elettroni
liberi nel blocco su cui avviene la diffusione, proprio come se si trattasse
di palle da biliardo. I fotoni di rinculo uscenti dal blocco costituiscono,
sotto questo punto di vista, la radiazione diffusa. Dato che il fotone uscente
trasferisce un po' della sua energia all'elettrone con cui entra in collisione,
il fotone diffuso deve avere un'energia minore E'; pertanto dovrà avere
una frequenza inferiore n' che implica una lunghezza
d'onda più elevata l'. Questa descrizione
rende conto almeno qualitativamente dello spostamento di lunghezza d'onda
Dl. Si osservi come questo modello a particelle
della diffusione dei raggi X sia diverso da quello basato sulla descrizione
ondulatoria.
Analizziamo quantitativamente una singola collisione fotone-elettrone.
La simulazione proposta rappresenta una collisione fra un fotone ed un elettrone;
si fa l'ipotesi che l'elettrone sia a riposo ed essenzialmente libero, cioè
non legato agli atomi del diffusore. Applichiamo a questa collisione la legge
della conservazione dell'energia. Siccome gli elettroni di rinculo possono
avere una velocità v paragonabile a quella della luce dobbiamo
usare l'espressione relativistica dell'energia cinetica dell'elettrone. Sfruttando
l'espressione E=hn ed il fatto che il calcolo dell'energia
cinetica deve tener presente che la massa varia con la velocità (ovvero
scrivendo l'energia cinetica nella forma Ec=Dmc2),
possiamo scrivere:
in cui il secondo termine del secondo membro rappresenta l'espressione relativistica
dell'energia cinetica dell'elettrone di rinculo, dove m è la massa
relativistica ed m0 la massa a risposo dell'elettrone. Sostituendo
c/l a n e c/l'
a n' si può scrivere:

Applichiamo ora la legge di conservazione della quantità di moto alla
collisione. Per prima cosa ci occorre un'espressione dell'impulso del fotone.
Se un oggetto assorbe totalmente un'energia U da un fascio parallelo
di luce che incide su di esso, il fascio luminoso, secondo la teoria ondulatoria
della luce, trasferisce simultaneamente all'oggetto un impulso dato da U/c.
Nella descrizione a fotoni immaginiamo che questo impulso venga trasportato
dai singoli fotoni, ognuno dei quali trasporta un impulso in quantità
p=hn/c, dove h è l'energia
del fotone. Così, se sostituiamo l a c/n,
possiamo scrivere:
La conclusione che l'impulso di un fotone sia dato da h/l
può anche dedursi dalla teoria della relatività.
L'espressione relativistica della quantità di moto dell'elettrone è
data da:
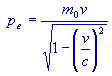
Per la conservazione della componente x della
quantità di moto possiamo scrivere:

e per la componente y:

Nostro immediato scopo è di trovare la variazione di lunghezza d'onda
dei fotoni Dl (cioè l'
- l), in modo da poterla confrontare ai risultati
sperimentali. Nell'esperimento di Compton non fu esaminato l'elettrone di
rinculo. È possibile eliminare due dei cinque parametri (l,
l', n, j, q) che compaiono nelle ultime
equazioni scritte. Eliminiamo n e q
che riguardano soltanto l'elettrone, riducendo così le equazioni ad
un'unica relazione tra i parametri.
Effettuando le operazioni algebriche necessarie, giungeremo a questo semplice
risultato:
![]()
Così lo spostamento Compton Dl dipende solo
dall'angolo di diffusione j e non dalla lunghezza
d'onda iniziale l. Quest'ultima equazione prevede,
entro gli errori, gli spostamenti Compton osservati sperimentalmente. Si noti
dall'equazione che Dl varia da zero (per j=0,
che corrisponde ad una collisione "di striscio") a 2h/m0c
(per j=180°, che corrisponde ad una collisione
"frontale" ove il fotone incidente rimbalza all'indietro).
Rimane da spiegare la presenza del picco per il quale la lunghezza d'onda
non varia nella diffusione. Si può spiegare questo picco come risultante
da una collisione fra fotoni ed elettroni legati a ioni del blocco su cui
avviene la diffusione. Nelle collisioni gli elettroni legati si comportano
come quelli liberi, con la differenza che la loro massa efficace è
molto maggiore. Ciò è dovuto al fatto che nella collisione rincula
tutto il complesso ionico. La massa efficace M per un diffusore di carbonio
è circa uguale alla massa di un nucleo di carbonio. Dato che questo
nucleo contiene 6 protoni e 6 neutroni, avremo approssimativamente M=12x1840m0=22.000
m0. Se sostituiamo m0 ad M nell'ultima equazione scritta,
vediamo che lo spostamento Compton per collisioni con elettroni strettamente
legati è estremamente piccolo, tanto da non potersi misurare.
 Dispositivo
sperimentale di Compton.
Dispositivo
sperimentale di Compton.