Distanza tra due punti
|
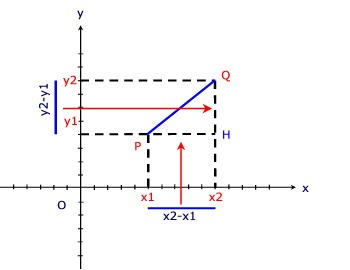
Applicando il teorema di Pitagora al triangolo PHQ, rettangolo in H si ottiene:
Casi particolariDue punti individuano un segmento parallelo all'asse x, come PH. La distanza si calcola pių rapidamente con la formula |x2-x1|. I due punti individuano un segmento parallelo all'asse y, come QH. La distanza si calcola pių rapidamente con la formula |y2-y1|. |
Punto medio di un segmento

Per determinare la posizione del punto medio basta osservare la figura e si ricava:
XM= |
XP + |
XQ - XP
2 |
= |
XP + XQ 2 |
YM= |
YP + |
YQ - YP 2 |
= |
YP + YQ 2 |
| M | ( |
XP + XQ 2 |
YP + YQ 2 |
) |
