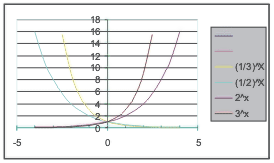
Christopher Kent Mineman - Didattica in rete

Funzioni esponenziali

Partiamo dall'analisi di quanto realizzato in Excel nel laboratorio di informatica:

X
(-2)X
(-1/2)X
(1/3)X
(1/2)X
2x
3x
-4
 0,0625 16 81 16 0,0625 0,012346
-3,5
 ? ? ... 11,31371 0,088388 0,021383
-3
 -0,125 -8   8 0,125 0,037037
-2,5
 ? ?   5,656854 0,176777 0,06415
-2
 0,25 4   4 0,25 0,111111
-1,5
 ? ?   2,828427 0,353553 0,19245
-1
 -0,5 -2   2 0,5 0,333333
-0,5
 ? ?   1,414214 0,707107 0,57735
0
 1 1 1 1 1 1
0,5
 ? ? 0,57735 0,707107 1,414214 1,732051
1
 -2 -0,5 0,333333 0,5 2 3
1,5
 ? ? 0,19245 0,353553 2,828427 5,196152
2
 4 0,25 0,111111 0,25 4 9
2,5
 ? ? 0,06415 0,176777 5,656854 15,58846
3
 -8 -0,125 0,037037 0,125 8 27
3,5
 ? ? 0,021383 0,088388 11,31371 46,76537
4
 16 0,0625 0,012346 0,0625 16 81
4,5
 ? ? 0,007128 0,044194 22,62742 140,2961
5
 -32 -0,03125 0,004115 0,03125 32 243
5,5
 ? ? 0,002376 0,022097 45,25483 420,8883

 

Proprietà di a x

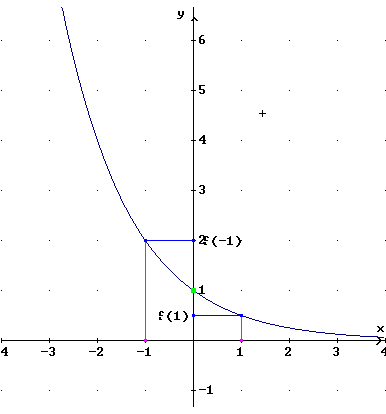
Modello di funzione esponenziale con base > 1

Modello di funzione esponenziale
con 0 < base <1Y=(1/2)X

 

Basi negative:

E' possibile calcolarna la potenza solo se l'esponente è un numero intero.
 

Basi tra 0 e 1:

All'aumentare dell'esponente decresce il valore dell'esponenziale. La funzione esponenziale risulta essere monotona decrescente.

Tende a + infinito se la x tende a - infinito. (Diverge a + infinito per x tendente a - infinito)

Tende a 0 se la x tende a + infinito. (Ammette per x tendente a + infinito l'asintoto orizzontale Y=0)
 

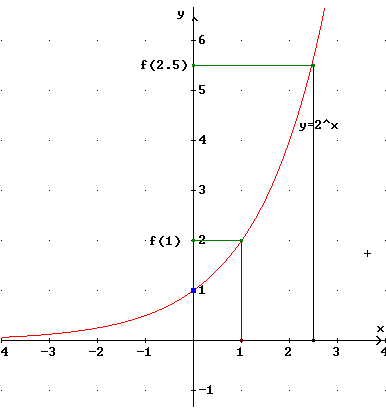
Basi > 1

All'aumentare dell'esponente cresce il valore dell'esponenziale. La funzione esponenziale risulta essere monotona crescente.

Tende a + infinito se la x tende a +infinito. (Diverge a + infinito per x tendente a +infinito)

Tende a 0 se la x tende a + infinito. (Ammette per x tendente a -infinito l'asintoto orizzontale Y=0)