A ognuno di noi è
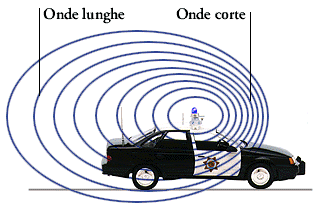
capitato di ascoltare il suono della sirena di un'auto della polizia:
quando la vettura si avvicina, il suono ci appare più acuto
di quello dell'auto ferma. Quando invece l'auto si allontana, il suono
ci appare più basso.
Ogni volta che ascoltiamo un suono emesso da una sorgente in movimento,
questo suono ci appare:
| più acuto | mentre la sorgente si avvicina, |
| più basso | mentre la sorgente si allontana. |
Questo "effetto" prende il nome di Effetto Doppler.
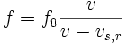
la formula scritta vale se la sorgente si sta allontanando dall'osservatore altrimenti al denominatore metteremo il segno più (+)
Attenzione però: quel che cambia è il suono udito, non il suono emesso. Il suono
di una sirenza di un'ambulanza, per esempio, rimane lo stesso, sia che
la vettura sia ferma sia che si stia muovendo.
Se riproduciamo la situazione con un diapason, che emette un suono di
frequenza ben definita f0
osserviamo che a un suono più basso corrisponde un suono con
una frequenza f
minore di f0;
al contrario, a un suono più acuto corrisponde una frequenza
f
maggiore di f0.
La differenza fra le due frequenze è legata alla
velocità della sorgente sonora: più veloce
è la sorgente sonora, più grande è la
differenza tra la frequenza udita e la frequenza emessa. In questa
equazione v
è la velocità del suono nell'aria, mentre vs,r è la velocità con cui la sorgente si avvicina o si allontana dall'osservatore.
Se la sorgente è in quiete ma è l'osservatore si sposta (avvicinandosi o allontanandosi) alla sorgente sonora, avremo ugualmente l'effetto doppler.
Il questo caso per determinare la frequenza apparente dobbiamo usare una formula diversa:
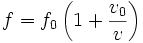L'equazione appena vista
è corretta nel caso in cui la velocità relativa
tra sorgente e rivelatore sia piccola rispetto alla velocità
del suono.Quanto prima riportato vale se ci avviciniamo alla sorgente, in caso contrario metteremo il segno meno tra i due termini presenti nella parentesi.