Moto di un punto materiale che percorre archi di circonferenza uguali in tempi uguali.
Il moto è pertanto caratterizzato dal fatto che la velocità scalare, ossia l'arco di circonferenza percorso ogni secondo, è costante nel tempo. Dalla geometria abbiamo che ad archi di circonferenza uguali si associano angoli al centro uguali e pertanto è immediato definire una nuova grandezza fisica:
LA VELOCITA' ANGOLARE.
La velocità angolare è l'angolo al centro sotteso nell'unità di tempo dal punto materiale w = Da / Dt o in termini infinitesimi w = da / dt
Se all'istante t=0 il punto materiale è situato nel punto Po(R;0) e il corpo si muove in senso antiorario allora la legge oraria dell'angolo descritto sarà:<α = ω t.
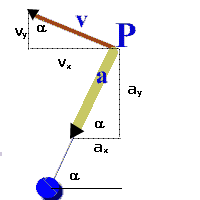 |
Si può dimostrare che l'accelerazione è sempre centripeta e la velocità sempre tantente alla traiettoria.
Si può facilmente ricavare l'espressione del modulo della velocità
V = Circonferenza / T (periodo ossia il tempo impiegato per descrivere una circonferenza)
|V| = 2 π R / T
ma ω = 2 π / T e quindi:
|V| = ωR
Il modulo dell'accelerazione vale ( non lo dimostro ora)
|a| = -ω2 R
Dalla trigonometria e dai ragionamenti fatti si ricavano immediatamente le leggi orarie:
| Posizione | X= R cos ω t |
| Y= R senω t | |
| Velocità | Vx= -ω R sen ω t |
| Vy= ω R cosω t | |
| Accelerazione | ax = - ω 2 R cos ω t |
| ay= - ω 2 R sen ω t |