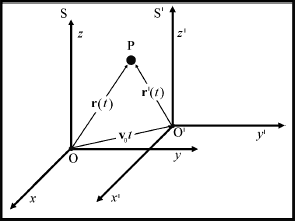
Sistemi di riferimento: moto rettilineo uniforme l'uno rispetto all'altro.Consideriamo due osservatori che analizzano l'evolversi di un evento connesso ad un oggetto in moto. Siano i due osservatori in moto l'uno rispetto all'altro, i modo tale da aver occupato all'istante t=0 la stessa posizione.
O' = O + V0 t. Se due osservatori solidali con i due sistemi di riferimento dovessero analizzare il moto di un punto mobile P, cosa ricaveranno? Prima di rispondere a questa domanda è opportuno scomporre il moto nelle sue componenti, supponendo che il sistema in moto si muova l'ungo l'asse x del sistema in "quiete". Consideriamo due casi:
Pertanto se dovessimo dalle leggi orarie ricavare le velocità ricordandoci che: v (dx/dt;dy/dt;dz/dt) essendo dx,dy,dz gli incrementi infinitesimali che avvengono nell'inervallo infinitesimo dt. V'(vx+ v0; vy; vz)=V+(v0;0;0) Mentre per l'accelerazione:
a'(dvx/dt;dvy/dt;dvz/dt)= a |
 Supponendo
che all'istante t=0 i due sistemi di riferimenti erano sovrapposti,
col passare del tempo si allontaneranno con
Supponendo
che all'istante t=0 i due sistemi di riferimenti erano sovrapposti,
col passare del tempo si allontaneranno con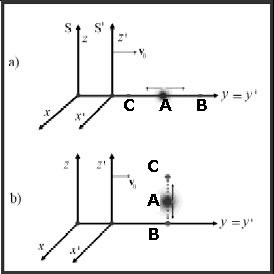 diverse
ascisse, anche se in ogni istante potranno confrontare i dati utilizzando
la seguente legge di trasformazione:
diverse
ascisse, anche se in ogni istante potranno confrontare i dati utilizzando
la seguente legge di trasformazione: