Chiameremo progressione geometrica quella successione in cui il rapporto tra un elemento e il suo precedente è costante.
Chiameremo tale coefficiente "ragione della progressione geometrica" e la indicheremo con "q".
Avremo: a n =an-1.q
È possibile determinare la relazione tra a n e n ?
Partendo dalla definizione possiamo ricavare l'espressione da associare all'elemento ennesimo della progressione geometrica: a1=a . . . a2=aq . . . a3=a q2. . .
e in generale . . . an=a q(n-1)
Come calcolare la somma dei primi n termini.
Ricordiamoci che:
(qn -1)/(q-1)=q n-1+q n-2+qn-3+ . . .+q+1
Ossia anche:
(1- qn)/(1-q)=1+q+q²+ . . .+q n-3+q n-2+qn-1
Pertanto abbiamo che:
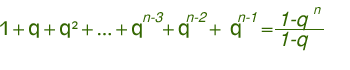 |
Consideriamo i primi n termini di una progressione geometrica:
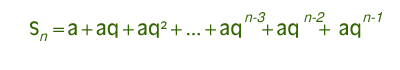 |
e quindi:
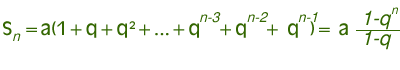 |
Altre regole utili:
Se conosco il valore di due termini, an e am è utile calcolare il loro rapporto in quanto:
an / am che vale sempre q m-n
Ricordarsi che:
per calcolare il limite per n tendente all'infinito della somma Σ an, osserviamo che se q è maggiore di 1 la progressione geometrica è divergente e quindi la somma tenderà all'infinito.
Se q è minore di 1 poichè qn tende a zero avremo che la somma sarà convergente e varrà:
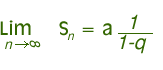
In questo caso la somma di infiniti numeri positivi da per risultato un numero finito.