Definizione di limite infinito:
Diremo che la successione è divergente ossia tende all'infinito per n tendente all'infinito e scriveremo :
se per ogni K positivo e grande a piacere si può determinare un numero M(K) grande e dipendente da K tale per cui per ogni n>M si abbia:
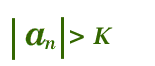
Negli esercizi di verifica dobbiamo verificare che partendo da 
e risolvendo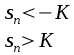
la disequazione associata
si ottiene che una soluzione sia del tipo
ESEMPIO
Verificare il seguente limite: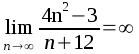 
Partendo dalla definizione scriviamo:
Nel nostro saso essendo il rapporto sempre positivo per n sufficientemente grande studieremo unicamente il numeratore di sn>K (il denominatore è sempre positivo) :
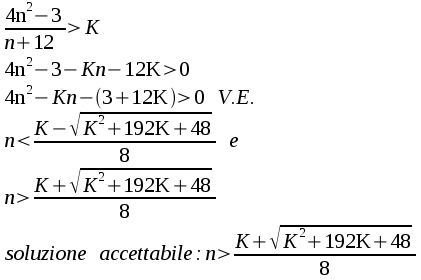
Pertanto, avendo trovato che la relazione d'ordine è verificata per n maggiore di M(K) [la soluzione trovata] abbiamo verificato che la successione è divergente.