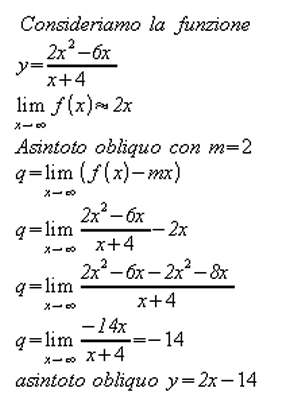CASO ASINTOTO VERTICALE

Diremo che una funzione → ∞ per x →x_o se per ogni K grande a piacere si  può determinare un intorno di x_o  tale per cui  per ogni x appartenente a tale intorno si abbia | f(x) | >K.

Non appartenendo x_o al dominio della funzione è opportuno analizzare separatamente il limite sinistro e il limite destro.

Otteniamo 4 casi:

1. f(x) → - ∞ per x → x_o da più
2. f(x) → + ∞ per x → x_o da più
3. f(x) → -∞ per x → x_o da meno
4. f(x) → +∞ per x → x_o da meno

 

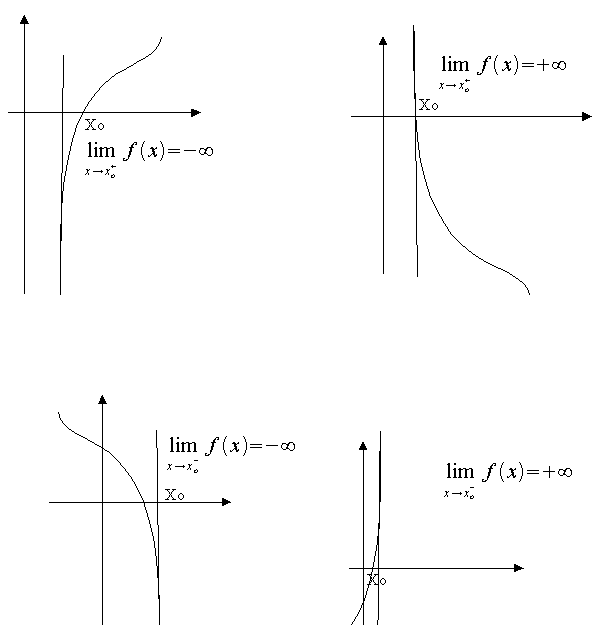
CASO ASINTOTO ORIZZONTALE

Diremo che una funzione tende al limite finito L per x → ∞, se per ogn ε piccolo a piacere si può determinare un N, dipendente da epsilon tale per cui  per ogni |x|>N si abbia ¦f(x) - L | < ε.

In questi casi chiameremo asintoto orizzontale la retta Y= L

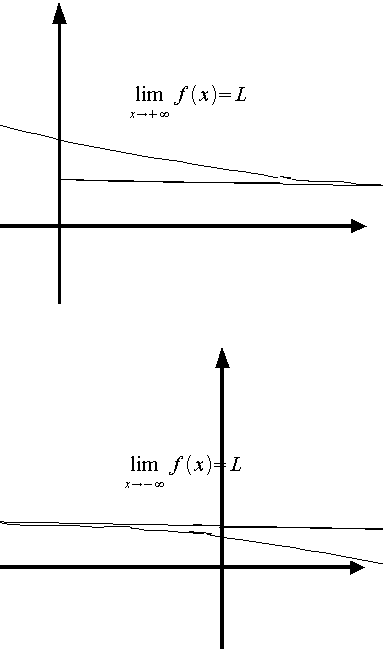
CASO ASINTOTO OBLIQUO

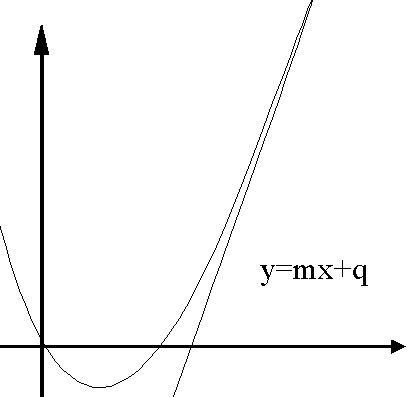
Parleremo di asintoto obliquo quando il limite per x → ∞ della funzione è asintotico a mx.
La funzione in questo caso tenderà all'infinito alla retta y=mx+q; dove m è il coefficiente dell'espressione asintotica e q si determina dal
limite per x → ∞ [f(x)-mx]

Segue un esempio (non guardare per il momento i calcoli).