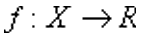Christopher Kent Mineman - Didattica in rete

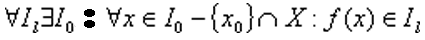DEFINIZIONE DI LIMITE FINITO

Sia f(x) una funzione definita in un insieme X, sottoinsieme di R, e a valori in R, in simboli

e x0 un punto di accumulazione per tende ad L al tendere di x a xo e si scrive: quando, per ogni ε piccolo a piacere, si può sempre trovare un intorno completo del punto x0 di ampiezza d dipendente da e, tale che per ogni x tale che xo - δ < x < xo +δ escluso eventualmente x0 , | f(x) - L | < ε

Ossia:

limite finito;

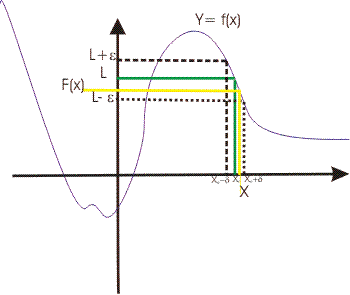
oppure:

quando, per ogni numero ε >0 esiste un numero δε tale che per ogni x appartenente all'intorno di x0,
Nella matematica infinitesimale siamo portati a studiare come dedurre le ordinate da assegnare alla funzione y=f(x) quando la x assume valori sempre più prossimi ad un dterminato valore x0. Studieremo le ordinate dedotte utilizzando la presente tecnica. Non si studia cosa avviene in un punto, ma come si comporta la funzione in un determinato intervallo. Si studiano andamenti e comportamenti in intervalli piú o meno estesi.