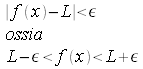Premessa
Fino ad oggi abbiamo sempre studiato le funzioni utilizzando il metodo deterministico.
Conoscendo la linea che si vuole associare ad una funzione e analizzandone le caratteristiche, sfruttando il concetto di luogo geometrico,
si ricava l'espressione della funzione e successivamente per disegnare la linea associata alla funzione ricavata applicavamo il metodo
della sostituzione puntuale.
Ad ogni x si associa una y e si rappresenta sul p.C. il punto associato a tale coordinata e ripetendo all'infinito questa tecnica si rappresente la funzione assegnataci.
Concetto di limite.
Consideriamo una funzione del tipo y=f(x) e immaginiamo che sia rappresentabile con la linea rossa.
Scegliamo un numero reale x0 appartenente all'insieme dei numeri reali e associabile ad un punto dell'asse delle ascisse. Di tale punto non vogliamo determinare la f(x0) ossia la y associata.
Ci domandiamo: Se utilizzassimo le x di un intorno completo di x0 e ne determinassimo le corrispondenti f(x) [y] potremmo determinare a quale y si sta avvicinando la funzione?
In altre parole è possibile dedurre la y da associare a x0 senza calcolarla ma analizzando solamente le f(x) ricavate in precedenza con la modalità sopra descritta?
Chiameremo Limite e lo indicheremo con L la y che pensiamo si debba associare alla x0 .
Il limite è pertanto una y dedotta e non calcolata.
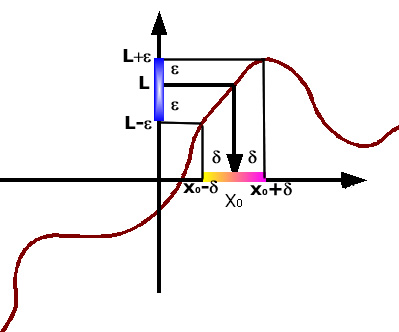
Dalla figura si evince che utilizzando le x appartenenti ad un intorno completo i x0 si devono determinare y tutte appartenenti ad un intorno completo di L.
Definizione di limite finito
Diremo che la funzione y=f(x) tende al limite finito L per x tendente a x0 e scriveremo: 
se per ogni intorno di L di ampiezza ε >0, ma piccolo a piacere, è possibile determinare un intorno di x0 di ampiezza δ tale per cui per ogni x di tale intorno si abbia
