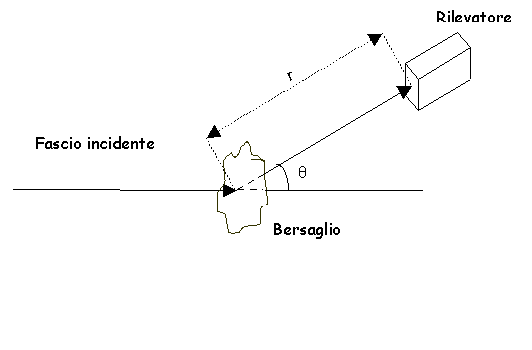
Riprendiamo la geometria di un esperimento di scattering:

Una sorgente emette un fascio che viene inviato contro un bersaglio che interagisce con il pennello deviandolo oppure diffondendolo o facendo altro. Poniamo un rivelatore (ortogonalmente alla direzione di diffusione) ad una distanza r dal punto in cui il bersaglio viene colpito dal pennello incidente; ipotizzando una simmetria cilindrica¹ possiamo individuare l’angolo tra il pennello diffratto e la direzione di incidenza come angolo di deflessione.

Per descrivere bene un esperimento di scattering dobbiamo in qualche maniera collegare i dati relativi al fascio incidente iniziale (che dovremmo conoscere per come produciamo il pennello) con quelli che rileviamo relativi al fascio finale, raccogliendo informazioni a diversi angoli di deflessione.

Introduciamo così il concetto di flusso, inteso però diversamente da come lo avete già visto, ad esempio, nel teorema di Gauss. Noi intenderemo per flusso una certa grandezza per unità di tempo. Ad esempio: il flusso di macchine che passano in una certa via è da intendere come numero di macchine che passano in un minuto. Il flusso di carica è da intendersi, in questo modo, come flusso di carica per unità di tempo, e cioè la corrente. Così come il flusso di energia, inteso come l’energia per unità di tempo, non è altro che la potenza. Oppure ancora il flusso relativo ad un liquido non è altro che la portata. Con il termine flusso quindi intendiamo sempre un qualcosa per unità di tempo.

Il flusso del pennello (iniziale o finale) non è altro quindi che la “quantità” di pennello che passa in un certo intervallo di tempo diviso l’intervallo di tempo stesso (quantità di pennello per unità di tempo). La quantità di pennello può essere calcolata attraverso una misura dell’energia, dell’intensità, o di altro.

Per il fascio incidente, che in generale si considera generato lontano dal bersaglio in modo da giungere come onda piana, è comodo utilizzare il flusso per unità di superficie e che indico con

dF₀/dS dove il pedice 0 sta ad indicare che sto considerando il pennello incidente e utilizzo la “d” davanti a flusso e superficie per indicare che sto considerando solo una piccola parte (di flusso e di superficie).

Per il fascio diffuso invece non ha più senso utilizzare il flusso per unità di superficie, per i motivi che ci hanno indotto ad introdurre l’angolo solido: dipenderebbe dalla distanza a cui pongo il rilevatore. Quindi ci è comodo utilizzare il flusso per unità di angolo solido che indico con .

Voglio trovare una relazione tra e dF₀/dS.

La cerco partendo dal problema di scattering “diretto”: conosco il bersaglio, so come interagisce con il fascio incidente, trovo una relazione tra e dF₀/dS e la generalizzo.

Osserviamo ora alcuni semplice esperienze di scattering e cerchiamo di descrivere quanto avviene.

1. Se inviamo un pennello di luce laser contro uno specchio (grande; come fatto in classe), il pennello verrà riflesso ad un angolo pari all’angolo di incidenza; questo vuol dire che il flusso iniziale è uguale a quello finale per un solo angolo di deflessione mentre altrove sarà nullo.

2. Se inviamo invece la luce contro una superficie scabra (carta da forno), questa diffonderà la luce tutto intorno in maniera uniforme. Infatti io vedo la luce da qualunque parte mi metto. Questo vuol dire che a qualsiasi angolo del semispazio di incidenza rileveremo sempre lo stesso flusso.

Osserviamo che:

nel caso della riflessione la relazione tra e dF₀/dS è diversa a seconda dell’angolo di deflessione . Infatti se chiamo l’angolo di riflessione, avremo che sarà nullo per ogni θ ad eccezione di dove avremo che tutto il fascio incidente viene tutto riflesso. Quindi possiamo pensare che dipenda da

Nel caso della diffusione da parte della superficie scabra l’intensità della luce che vede il nostro occhio è minore, perché la luce viene distribuita uniformemente in tutto lo spazio (corrispondente ad un angolo solido di 4π).

Il flusso di energia rilevato (in entrambi i casi) dipende dalla dimensione della sezione del fascio.

Scrivo in formula quella che potrebbero essere le relazioni.

Per lo specchio:

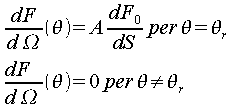
Per la superficie scabra:

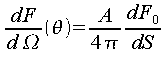
e il pennello viene distribuito uniformemente in tutto lo spazio.

Ma queste formule sono relativamente semplici perché abbiamo considerato delle situazioni elementari, avendo fatto alcune semplificazioni.

Innanzitutto abbiamo considerato un bersaglio singolo. Ma negli esperimenti di scattering di fisica il bersaglio non è un “blocco” solo di materia o altro, ma si presuppone sia composto da tanti bersaglini di piccole dimensioni, tutti uguali tra loro. Le dimensioni del singolo bersaglino, che viene chiamato con il nome di “centro diffusore” sono minori della sezione del fascio incidente.

In questo modo non tutto il fascio incidente interagirà con i centri diffusori, quindi ci si aspetta che una parte del fascio passi inalterata oltre il bersaglio mentre solo una parte interagisca con i centri diffusori. Ciò che rileveremo, cioè il flusso per unità di angolo solido, è proporzionale al numero di centri diffusori che il fascio incontra e alla superficie che mostrano al fascio incidente.

Supponendo che i centri diffusori siano disposti regolarmente all’interno del bersaglio, il numero N di centri diffusori che vengono investiti dal fascio dipende dalla densità n, dallo spessore h del bersaglio e ovviamente dalla sezione A del fascio incidente. Cioè:

N=nhA

Per semplicità si studia la singola interazione, ma la relazione finale, che è quella che si ottiene sperimentalmente da un esperimento di scattering, è ottenuta moltiplicando la singola interazione per il numero N dei centri diffusori.

Per ridurre al minimo la probabilità che il pennello possa interagire con più di un centro diffusore si è soliti considerare bersagli con uno spessore “sottile”.

Da ora in poi considereremo sempre il bersaglio costituito da molti centri diffusori con le medesime caratteristiche e distribuiti regolarmente all’interno del bersaglio; il pennello incidente avrà una sezione A maggiore delle dimensioni del singolo centro diffusore.

Quindi una relazione generale tra il flusso iniziale e quello rilevato dovrà tenere conto di tutto quanto detto: del numero di centri diffusori colpiti dal fascio N=nhA, dalla posizione di rilevazione (che in simmetria cilindrica dipende solo dall’angolo” θ) e dal tipo di interazione avvenuta, cioè da come il bersaglio interagisce con il tipo di pennello incidente, e quindi potrebbe dipendere da grandezze come carica, massa, velocità del pennello incidente o altro. In formula possiamo riassumere il tutto scrivendo:

(1)

dove è la funzione di proporzionalità che racchiude in sé tutte le caratteristiche di cui sopra ed è chiamata sezione d'urto differenziale. Questa grandezza ha le dimensioni di una superficie su un angolo solido, come si può dedurre da una analisi dimensionale della (1); ci dice quale deve essere la superficie del singolo centro diffusore vista dal pennello che deve essere colpita affinché ci sia una deflessione in una certa direzione compresa tra ; trattandosi di una superficie dovrà essere sempre positiva quindi ne consideriamo sempre il modulo .

Oltre alla sezione d'urto differenziale esiste un’altra grandezza, la sezione d'urto totale (σ), che ci dice qual è la superficie totale da colpire affinché ci sia una interazione rilevabile in una qualsiasi direzione.

È legata alla sezione d'urto differenziale dalla relazione:

La sezione d'urto totale ha le dimensioni di una superficie e, come tale, anch’essa è sempre maggiore di zero.

Esempi di sezione d'urto

Bersaglio in cui il singolo centro diffusore è uno specchio di superficie l² perpendicolare alla direzione di incidenza del fascio.

Interazione: riflessione di tutto il fascio ad un angolo

Superficie mostrata al fascio incidente: la sua superficie l²

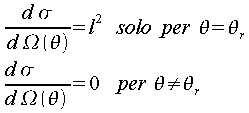
Come leggerlo?

La superficie da colpire affinché il rilevatore possa rilevare qualcosa ad un angolo pari esattamente all’unico angolo di riflessione è proprio la superficie dello specchio; la superficie da colpire affinché si possa rilevare qualcosa ad angoli diversi da è invece nulla, come dire che non esiste alcuna superficie da colpire perché non c’è interazione.

Come lo so? È la superficie da colpire affinché ci sia una interazione (qualsiasi). È uguale alla sezione d'urto differenziale perché ho una sola interazione possibile: la riflessione.

La relazione tra flusso incidente e flusso rilevato è

ovviamente solo per l’angolo

Bersaglio in cui il singolo centro diffusore è una superficie scabra (pezzettino di muro) di superficie l² perpendicolare alla direzione di incidenza del fascio.

Interazione: il muro diffonde uniformemente in tutto il semispazio di incidenza, pari ad un angolo solido Ω=2π.

Attenzione: dire che il fascio viene diffuso in tutto il semispazio di incidenza vuol dire considerare θ appartenente ad un certo intervallo, in questo caso (perché c’è simmetria cilindrica).

Superficie mostrata al fascio incidente: la sua superficie l²

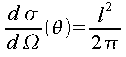
La relazione tra flusso incidente e flusso rilevato è allora

Osservazione: la sezione d'urto totale è la stessa sia per lo specchio sia per il muro

Esempi di sezione d'urto totali:

Bersaglio costituito da tanti specchi piani di superficie l² ruotati di un angolo α rispetto alla direzione di incidenza del fascio.

Bersaglio costituito da tante superfici scabre di superficie l² ruotati di un angolo α rispetto alla direzione di incidenza del fascio

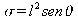
È la stessa sezione d'urto perché la superficie che “mostrano” al fascio incidente è la stessa e una volta che il fascio incontra la superficie sappiamo (perché conosciamo il bersaglio) che avverrà sicuramente una interazione.

Bersaglio costituito da tanti specchi cilindrici posti con l’asse del cilindro ortogonale alla direzione di incidenza; i cilindri hanno altezza l e raggio di base r.

cioè il fascio incidente “vede” un rettangolo di dimensioni lx2r.

bersaglio costituito da tante sferette riflettenti di raggio r:

Il calcolo delle sezioni d'urto differenziali richiede dei calcoli decisamente più complicati.