L’esperimento di Geiger e Marsden

Quello che viene chiamato scattering di Rutherford è il risultato di una serie di esperimenti eseguiti da Geiger e Marsden a partire dal 1909 sullo studio della diffusione della radiazione α da parte di una sottile lamina metallica; questi esperimenti furono i prototipi di tutti gli esperimenti di scattering.

Un po’ di storia

Alcuni esperimenti all’inizio del secolo scorso avevano mostrato che facendo incidere della radiazione β su una lamina di metallo, una forte radiazione emergeva dallo stesso lato della lamina da cui proveniva il fascio incidente; alcuni di questi esperimenti sembravano addirittura mostrare che questa radiazione non fosse una radiazione secondaria ma fosse la stessa radiazione incidente che veniva scatterata dalla lamina e quindi riflessa.

Geiger e Marsden, su suggerimento di Rutherford, volevano verificare se anche la radiazione α potesse avere un comportamento analogo; i loro primi esperimenti infatti erano volti proprio alla ricerca di una “riflessione” della radiazione α da parte di lamine di metallo.

In una camera a vuoto essi inviarono un pennello di alfonio (radiazione α) collimato su bersagli di diverso materiale (sottili lamine di oro, argento, rame e alluminio) rilevando il pennello diffuso su uno schermo in grado di ruotare intorno al bersaglio. Il rivelatore consisteva in uno schermo di solfuro di zinco che, interagendo con l’alfonio, produceva una scintillazione per ogni particella α giunta.

I risultati degli esperimenti confermarono quanto previsto nel senso che, analizzando la distribuzione angolare del pennello, si osservò che sebbene la maggior parte del pennello di alfonio passasse oltre la lamina sottile senza subire deflessione o con una lieve deflessione (angoli di qualche grado), era comunque presente un debole flusso anche ad angoli elevati, maggiori di 90° riemergendo dal lato incidente.

Nel dettaglio

L’apparecchiatura originale con cui vennero fatti questi esperimenti era semplice; Geiger e Marsden la descrivono così nel loro articolo “The laws of deflection of α particles through large angles” del 1913: “L’apparato usato consisteva principalmente in una robusta scatola di metallo di forma cilindrica B che conteneva la sorgente di particelle¹ α R, il foglio bersaglio F e un microscopio M attaccato rigidamente allo schermo S di solfuro di zinco². La scatola B era fissata ad una piattaforma circolare graduata A che poteva ruotare per mezzo di un giunto a tenuta d’aria C. Ruotando la piattaforma, la scatola e il microscopio ruotavano con lei, mentre foglio diffusore e la sorgente rimanevano nella stessa posizione, essendo attaccati al tubo T fissato alla base L. La scatola era chiusa da un vetro smerigliato P e al suo interno poteva essere fatto il vuoto tramite il tubo di aspirazione T.”

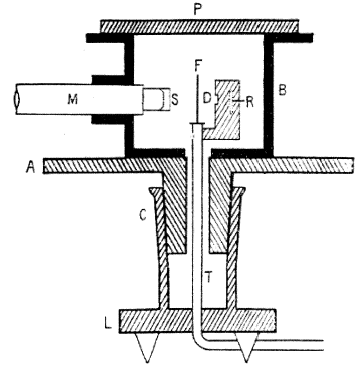
E ancora: “La sorgente di particelle α consisteva in un piccolo tubo di diametro di circa 1 mm riempito di radon… Per mezzo di un diaframma posizionato in D un sottile fascio di particelle veniva diretto ortogonalmente al foglio F . Ruotando il microscopio le particelle α diffuse in diverse direzioni potevano essere osservate sullo schermo S… la piccolezza degli effetti per grandi angoli di deflessione richiedeva piccole distanze schermo-foglio e foglio-sorgente; in alcuni esperimenti la distanza tra la sorgente e il foglio diffusore era di 2.5 cm e lo schermo si muoveva su una circonferenza di raggio di 1.6 cm.”

Geiger e Marsden fecero più esperimenti osservando lo schermo a diversi angoli di deflessione da 5° a 150°, mantenendo costante la durata dell’esperimento. Essi osservarono che il numero di particelle diffuse diminuiva molto rapidamente con l’aumentare dell’angolo, trovando però numerose tracce anche a grandi angoli. Nel loro primo articolo su questo argomento “On a diffuse reflection of the α particles” del 1909 (Su una riflessione diffusa delle particelle α) scrissero: “Nei seguenti esperimenti sono state trovate evidenti conclusioni dell’esistenza di una riflessione diffusa delle particelle α. Una piccola frazione di particelle α incidenti contro una lamina di metallo cambiano la loro direzione a tal punto che emergono di nuovo dal lato di incidenza.”

Questo era strano perché il foglio metallico sembrava praticamente ininfluente sulla quasi totalità delle pennello, mentre per una piccola parte risultava impenetrabile. Rutherford a tale proposito disse: “…era l’evento più incredibile che mi fosse mai capitato di osservare. Era come se una granata da 15 pollici [circa 38 cm], sparata contro un pezzo di carta velina avesse rimbalzato e colpito chi l’aveva sparata”.

I risultati dei primi esperimenti di Geiger e Marsden sono riportati nella tabella seguente.

Figura 2: tabelle originali

Prima di analizzare i risultati osserviamo le tabelle.

I dati sono suddivisi in due gruppi: da 150° a 15° e ancora da 30° a 5°. Questo perché sono state usate due sorgenti di radon di diversa intensità per permettere un corretto conteggio. Infatti le scintillazioni erano contate direttamente “a vista” dagli sperimentatori che dovevano “allenare” i loro occhi all’oscurità stando un po’ di tempo (circa mezzora) completamente al buio; questo poneva dei limiti di conteggio: Geiger e Marsden stessi indicarono come limite massimo 90 scintillazioni al minuto (per permettere di contarle) e come limite minimo 5 scintillazioni al minuto. Quindi per grandi angoli (da 15° a 150° dove arrivavano meno particelle) doveva essere utilizzata una sorgente di elevata intensità, mentre per piccoli angoli (tra 5° e 30°), dove il flusso era elevato, utilizzarono una sorgente meno intensa. Si può intuire che sono state usate sorgenti di diversa intensità dalla diversità di conteggio per gli stessi angoli (confronta 15°, 22.5° e 30°).

I dati sono espressi semplicemente in numero di scintillazioni (in altri esperimenti successivi sono espresse le scintillazioni per minuto). Se lo spessore del bersaglio è sottile allora il numero di scintillazioni è direttamente proporzionale alla sezione d'urto differenziale.

Per alcuni angoli di deviazione Geiger e Marsden hanno indicato dei valori non interi: di certo un numero decimale di scintillazioni non sta ad indicare una frazione di scintillazione. Il dato scaturisce dal fatto che Geiger e Marsden, contando le scintillazioni a vista, potevano commettere errori di conteggio per cui il numero scritto in tabella è il risultato di una analisi degli errori di conteggio.

I risultati delle esperienze di Geiger e Marsden diedero risultati solo in parte interpretabili secondo il modello di atomo allora in vigore; con tale modello si riusciva infatti a giustificare l’allargamento/sparpagliamento del fascio ipotizzando numerosi scattering successivi. Ma questo procedimento non giustificava la presenza di un certo numero di scintillazioni ad angoli molto grandi rispetto alla direzione originaria: la probabilità di trovare segnale ad angoli maggiori di 90° era molto più bassa di quella rilevata sperimentalmente (secondo alcuni calcoli la probabilità era dell’ordine di 10^-3518 contro 10^-4 circa trovato sperimentalmente). Da qui furono formulate delle ipotesi che portarono ad un nuovo modello atomico che permise di ricavare previsioni confrontabili con i risultati degli esperimenti.

Ipotesi di Rutherford

Nell’articolo “The scattering of α and β particles by matter and the structure of the atom” del 1911 Rutherford sviluppò una teoria per spiegare i risultati a grandi angoli dello scattering di Geiger e Marsden secondo la quale le deflessioni a grandi angoli erano dovute ad un singolo urto.

Affinché ciò avvenga è necessario che lo spessore del bersaglio sia sottile così che la possibilità di un secondo urto violento sia piccola. (Se, per esempio, la probabilità di una singola deflessione ad un angolo Φ nell’attraversare uno spessore h è 1/1000, la probabilità di due deflessioni successive ciascuna sempre di valore Φ è 1/10⁶, quindi molto piccola.)

Per spiegare ciò Rutherford ipotizza l’atomo costituito da un nucleo centrale di dimensioni molto piccole ed elettricamente carico, così che il nucleo possa essere sede di un intenso campo elettrico; il nucleo è circondato da particelle cariche di segno opposto alla carica nucleare, distribuite uniformemente in una sfera di raggio R intorno al nucleo così che l’atomo è globalmente neutro.

Poiché la maggior parte della massa è concentrata nel nucleo Rutherford ipotizza che l’urto violento sia proprio con il nucleo stesso, tralasciando l’interazione con gli elettroni. In questo modo l’unica forza agente nell’interazione tra l’alfonio (che ricordiamo era dotato di carica positiva) e il bersaglio è la forza elettrostatica, espressa dalla legge di Coulomb:

la forza che si esercita tra due cariche q₁ e q₂ poste ad una distanza r vale (in modulo)

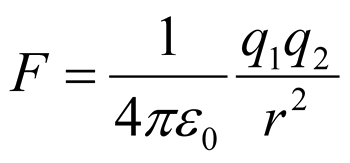
dove ε₀ è la costante dielettrica del vuoto³. La forza di Coulomb è una forza centrale.

Analisi esperimento di Rutherford

Rivediamo l’esperimento di scattering di Geiger e Marsden tenendo conto innanzitutto che i pennelli materiali, di cui l’alfonio ne è un esempio, si comportano come onde e quindi possiamo rappresentarli attraverso l’equazione dell’onda piana:

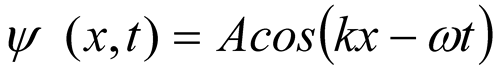
dove A è l’ampiezza dell’onda, k è il numero d’onda dato da

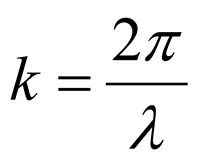
e ω è la frequenza angolare

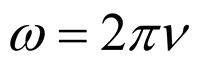
Innanzitutto studiamo il comportamento asintotico pennello di alfonio incidente ψ_inc cioè studiamo come si comporta lontano dal potenziale coulombiano V(r). Assumiamo che il pennello si avvicini al bersaglio da sinistra lungo l’asse che abbiamo scelto essere la direzione di propagazione dell’onda. Per grandi valori negativi di t il pennello non risente ancora del potenziale coulombiano, trovandosi ancora lontano dall’origine [V(r) è praticamente zero quando si è sufficientemente lontani dall’origine]; il suo comportamento è descritto dall’equazione delle onde vista sopra e possiamo scrivere

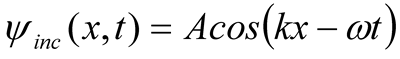
Quando l’onda raggiunge la regione sotto l’influenza del potenziale, la sua struttura si complica, per poi semplificarsi nuovamente per grandi valori di t, ossia lontano dall’influenza del centro coulombiano.

Per grandi valori di t, a grande distanza dal centro diffusore, l’onda è data dalla sovrapposizione dell’onda trasmessa che continua a propagarsi nella direzione positiva di x a cui però va sommata anche l’onda che è stata sottoposta al potenziale.

Poiché il potenziale è centrale, la parte dell’onda scatterata manterrà la simmetria centrale e sarà quindi un’onda sferica:

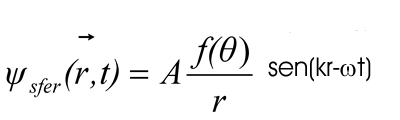
Per cui l’onda finale a grandi t, data dalla somma dell’onda piana con l’onda sferica, sarà:

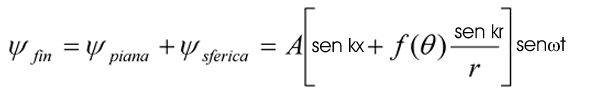
Disegno

Il termine ψ_sfer rappresenta un’onda sferica che nasce dal centro delle forze nel momento in cui questo viene investito dall’onda incidente. Notiamo che l’onda scatterata ha una ampiezza che dipende da due fattori: f(θ) e 1/r.

La dipendenza da è una conseguenza della conservazione dell’energia. Infatti sui fronti d’onda, che per le onde sferiche sono superfici sferiche centrate nell’origine dell’onda, l’energia deve essere costante. Allora anche l’intensità dell’onda, ossia l'energia che attraversa l’unità di superficie (ortogonale alla direzione di propagazione) nell'unità di tempo, deve essere costante; poiché la sfera aumenta la propria superficie in modo proporzionale a r² (l’area di un fronte d’onda di raggio r è 4πr²) l’intensità deve decrescere come 1/r². Infine, visto che

ossia l’intensità è proporzionale al quadrato dell’ampiezza dell’onda, ecco che l’ampiezza deve decrescere come 1/r.

La funzione f(θ), chiamata ampiezza di scattering, contiene tutte le informazioni sulla natura e il tipo di interazione perché è l’unica a dipendere dal potenziale V(r); ci dice cioè come sarà in definitiva l’onda dopo lo scattering (se non ci fosse le interazioni sarebbero tutte uguali).

Vediamo insieme da quali fattori può dipendere l’ampiezza di scattering.

dipende dall’angolo θ di deflessione⁴; questo vuol dire che l’onda sarà diversa a seconda dell’angolo a cui la rileviamo.

Dipende dalla velocità con cui arriva l’onda incidente e quindi dalla sua energia (o frequenza);

Dipende dal tipo di interazione che sappiamo essere di tipo elettrostatico, quindi dipenderà dalla carica dell’onda incidente e da quella del centro diffusore; inoltre f(θ) avrà “ricordo” della legge di Coulomb portandosi dietro la costante dielettrica del vuoto ε₀.

Proviamo ora a trovare una combinazione dei parametri appena elencati in modo che l’ampiezza dell’onda f(θ)/r sia adimensionale.

Chiamiamo q₁ la carica dell’onda incidente e q₂ quella del centro diffusore:

[ε₀]=(carica)²/(forza x lunghezza²)=(carica)²/(energia x lunghezza)

[E]=(energia)

[q₁]= (carica)

[q₂]= (carica)

[r]=(lunghezza)

[θ]= (radianti)……

L’unica soluzione, ovviamente ponendo r al denominatore, è data da

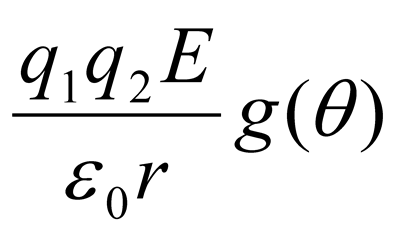
dove abbiamo lasciato una dipendenza generica da θ sia perché i radianti “non hanno dimensione” quindi non possiamo sapere se θ deve comparire al numeratore o al denominatore…; la funzione g(θ) è ricavabile attraverso calcoli partendo dai dati sperimentali.

Dalla formula sopra possiamo ricavare

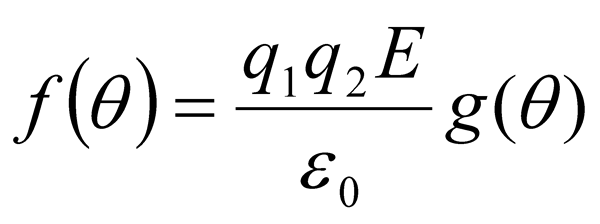
È intuitivo che la funzione f(θ) debba essere legata alla sezione d'urto differenziale, poiché conoscendo come viene diffusa l’onda, sappiamo indirettamente come il bersaglio devia il fascio durante l’interazione; si può dimostrare che

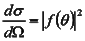
Per cui la sezione d'urto dello scattering che stiamo studiando è del tipo

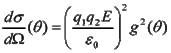
La sezione d'urto differenziale di Rutherford

Con le ipotesi da lui fatte e attraverso una analisi dettagliata dei dati sperimentali Rutherford trovò che la sezione d'urto differenziale relativa allo scattering di un pennello di alfonio da parte di una lamina di metallo è

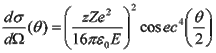
dove ha semplicemente indicato con ze e Ze le cariche dell’alfonio e del nucleo dell’atomo di cui è costituito il bersaglio.

Questa sezione d'urto differenziale ha molte caratteristiche interessanti:

È proporzionale a

cosec⁴(θ/2)

quindi decresce molto rapidamente al crescere di θ. Se θ è molto piccolo questo equivale a dire che la sezione d'urto differenziale è proporzionale a ossia è proporzionale a 1/θ⁴; questo spiega perché la maggior parte del pennello passa indisturbata. La dipendenza da cosec⁴(θ/2) non è tipica solo di questo tipo di interazione: per esempio lo scattering da un paraboloide di rotazione rigido ha una sezione d'urto differenziale con lo stesso tipo di dipendenza da θ. Però in questo caso non avremmo dipendenza né dall’energia del pennello incidente né dalle carica in quanto si tratterebbe di un urto rigido.

È direttamente proporzionale al quadrato della carica del nucleo del bersaglio e al quadrato della carica dell’alfonio; quindi è indipendente dal segno delle rispettive cariche. Anche conoscendo il segno della carica dell’alfonio dai dati di questi esperimenti non è possibile determinare il segno della carica del nucleo.

È inversamente proporzionale al quadrato dell’energia dell’alfonio; ciò significa che tanto più l’alfonio incidente è energetico tanto meno risulta deviato.