La razionalizzazione é l'insieme delle tecniche da mettere in essere per ottenere frazioni con denominatori razionali partendo da frazioni aventi termini irazionali al denominatore.
Ricordarsi che é possibile razionalizzare anche il numeratore (lasciando i termini irrazionali al denominatore).
Studieremo ora le tecniche piú utilizzate e imposteremo esercizi in cui si richiederà la razionalizzazione del numeratore e/o del denominatore.

monomio irrazionale

Distingueremo due sottocasi:
1º radice quadrata
2º radice con indice maggiore di 2

Primo caso: radice quadrata

Sistemare il denominatore potando fuori di radice il possibile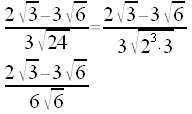
Moltiplicare numeratore e denominatore per la radice presente al denominatore e fare i calcoli.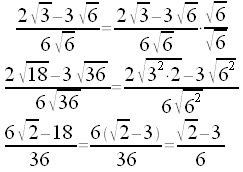

Secondo caso: radice ennesima

Sistemare il denominatore potando fuori di radice il possibile Moltiplicare numeratore e denominatore per la radice presente al denominatore elevando ogni monomio presente per la differenza "indice - esponente" Fare i calcoli e concludere

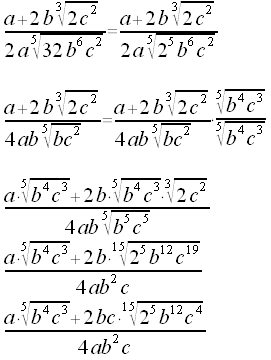Binomio con al piú due radici quadrate

Ricordandoci che: a2-b2=(a+b)(a-b) dobbiamo moltiplicare sia il numeratore che il denominatore per il binomio presente al denominatore cambiando il segno tra i due termini. quindi moltiplicare e sistemare la frazione.

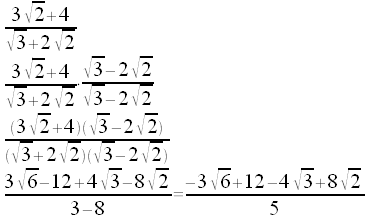Binomio trasformabile in differenza di cubi

Ricordandoci che: a3-b3=(a-b)(a2+ab+b2) dobbiamo moltiplicare sia il numeratore che il denominatore per il trinomio(falso quadrato). quindi moltiplicare e sistemare la frazione.
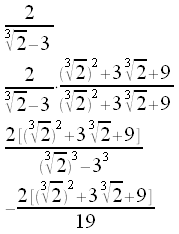