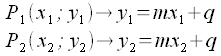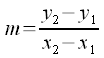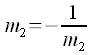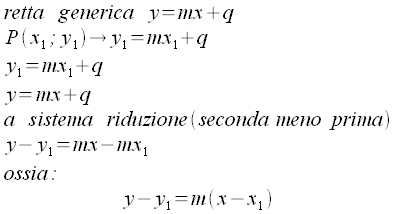Christopher Kent Mineman - Didattica in rete

Appartenenza

Ricordiamoci che se un punto appartiene ad una retta di cui conosciamo l'equazione, sostituendo le coordinate del punto alla x e alla y dell'equazione si deve ottenere una identità.

Se dobbiamo verificare che il punto di coordinate P₁(X₁;Y₁) appartiene alla retta di equazione Y=mX+q, dovremo verificare che:
Y₁=mX₁+q

RETTA PASSANTE PER DUE PUNTI ASSEGNATI

Per determinare l'equazione della retta passante per due punti sfrutteremo la proprietà sopra enunciata. Sostituendo le coordinate nell'equazione generica otteniamo un sistema a due incognite m e q. Risolvendo questo sistema otterremo l'equazione della retta cercata.

Coefficiente angolare

Per determinare il coefficiente angolare della retta passante per due punti è sufficiente utilizzare la formula che dimostreremo: Siano P₁(x₁;y₁) e P₂(x₂;y₂) i punti per cui deve passare la retta di cui vogliamo determinare il coefficiente angolare. Avremo:

e col metodo di riduzione (2° equazione - 1° equazione) :

RETTE PARALLELE - PERPENDICOLARI

Due rette sono parallele solo se hanno lo stesso coefficiente angolare (conseguenza immediata dalla definizione di retta).

Possiamo facilmente dimostrare che due rette sono perpendicolari se hanno i coeffiocenti angolari con

RETTA PER UN PUNTO

Per un punto passano infinite rette (fascio di rette con centro proprio). Infatti se imponiamo il passaggio per un punto e mettiamo a sistema la condizione trovata ricaviamo l'equazione riportata sui libri di testo.

Equazione della retta generica passante per il punto P.