Cos'è la retta?
A questa domanda in generale seguono risposte fantasiose del tipo: Linea diritta, linea dell'orizzonte, un insieme infinito di punti tutti allineati.
Nessuno è in grado di definire la retta. E' più facile definire il segmento come la geodetica tra due punti sul piano (la linea più corta che congiunge due punti). Per estensione potremmo definire la retta come la geodetica tra due punti posti da banda opposta all'infinito.
Assurdo!!
Euclide ha postulato:
La retta esiste e per due punti passa una sola retta.
In testa abbiamo ben presente cosa intendiamo per retta, ma non siamo in grado di definirla. Meglio postularne l'esistenza.
La retta esiste, ossia in ciascuno di noi e ben chiaro cosa vogliamo intendere quando parliamo di retta.
Per dirla con Euclide, si deve postularne l'esistenza e inoltre affermare per due punti passa una e una sola sola retta.
Interpretandola come luogo geometrico dei punti del piano e associando ad ogni punto una coppia ordinata di numeri reali è possibile associare ad ogni retta un'equazione a due variabili del tipo:
ax+by+c=0
se a=0retta parallela all'asse x riscrivibile, ponendo k= -c/b come:
x=k
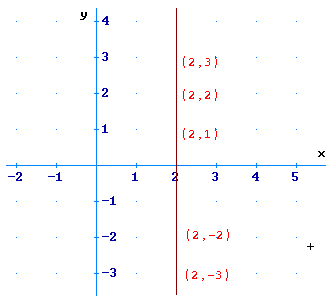
retta parallela all'asse y riscrivibile, ponendo k= -a/b come:
y=k
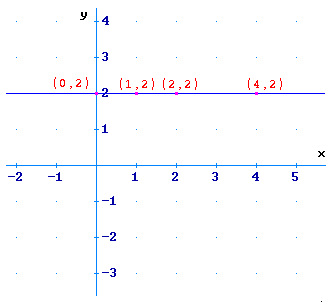
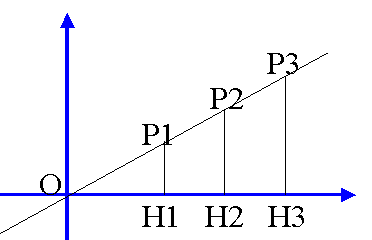
retta passante per l'origine del sistema di assi cartesiani riscrivebile, ponendo m= -a/b
y=mx
negli altri casi
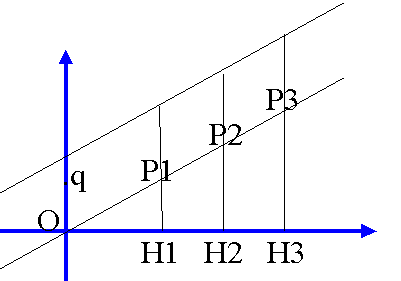
retta generica esplicitabile, ponendo m=-a/c e q=-c/a
y=mx+q