Testo

Determinata la parabola avente il vertice nel punto V(1;4) e passante per il punto K(2;3); sia A il punto di intersezione con l'asse delle ordinate e B il punto di intersezione con il semiasse positivo delle ascisse.
Preso un punto P appartenente alla parabola e situato nel primo quadrante determina in quale posizione l'area del triangolo ABP risulta essere massima.

Impostazione problema

Determiniamo l'equazione della parabola:

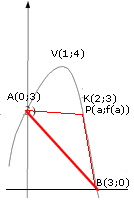1. Associamo al punto mobile le coordinate P(a;-a²+2a+3)
2. La retta AB ha equazione y=-x+3 (fare il passaggio per i due punti).
3. L'insieme di variabilità della variabile 'a': 0<a<3

Calcoliamo ora l'area del triangolo PAB

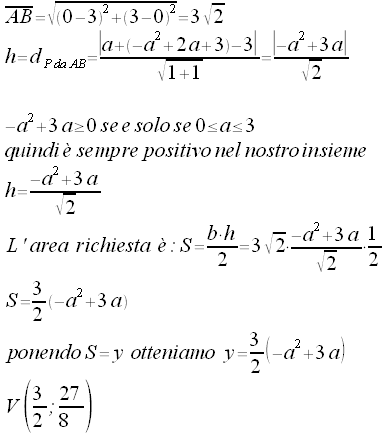Risoluzione La relazione trovata è associabile all'equazione di una parabola con la concavità rivolta verso il basso. Il punto di ordinata massima (superficie massima) lo avremo pertanto nel punto P(3/2;15/4) il vertice della funzione superfice non c'entra con il vertice della parabola iniziale