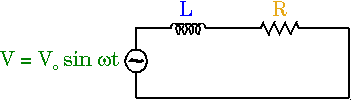
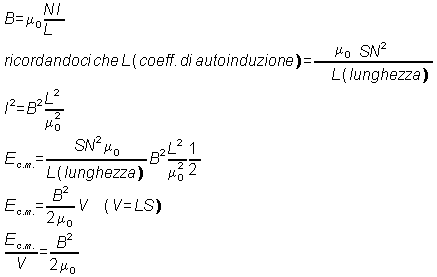Consideriamo un circuito in cui vi siano in serie una resistenza e un solenoide e alimentato da un generatore di corrente continua.
Alla chiusura del circuito la corrente che passa nel solenoide origina nei primi istanti un campo magnetico variabile, variando la corrente da 0 al suo valore massimo I=V/R. Questo determina l'insorgere di una contro forza elettromotrice che all'inizio rallenta il fluire della corrente.
Dalle leggi di Kirchoff sappiamo che il circuito è equivalente ad un circuito resistivo alimentato da due generatori di tensione: V e il generatore indotto associato al solenoide V= - L dI/dt.
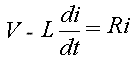
Analogamente al caso del circuito RC possiamo ricavare una soluzione qualitativa di questa equazione nel caso in cui V= Vo sen ω t e supponendo che in prima istanza in assenza dell'induttore anche I= Io sen ω t .
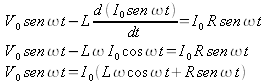
Pertanto anche in questo caso la corrente risulta essere non in fase con il potenziale e la resistenza (impedenza) dipende in questo contesto anche da L e da ω .
Per ricavare l'energia presente all'interno di un campo magnetico consideriamo un circuito elettrico costituito da un solenoide in serie con una resistenza connesso ad un generatore di tensione.
Possiamo supporre che il solenoide possa essere considerato alla stregua di un secondo generatore in serie (per Faraday Neumann).

Questa Energia messa a disposizione dal generatore di corrente in parte è assunta dalla resistenza che lo dissipa come energia termica e la restante parte viene ceduta al solenoide che lo utilizza per generare e mantenere il campo magnetico.
Pertanto l'energia del campo magnetico risulterà essere: ![]()
Ora per determinare l'energia per unità di volume operiamo in questo modo: