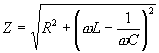La corrente è alternata. Oscilla continuamente con legge sinusoidale.
Con la corrente alternata abbiamo elettroni che oscillano, spostandosi avanti e indietro 50 o 60 volte al secondo.
Non abbiamo elettroni in moto che attraversino una superficie e pertanto come definire l'intensità di corrente?
Indirettamente sfruttando gli effetti termici.
Essendo cariche in moto dissiperanno energia accumulata e l'energia istantanea complessivamente dissipata si ricava dalla legge di Joule
W= I2R = Io 2 R sen 2ωt
Se rappresentiamo sul piano cartesiano il valore della potenza dissipata in un intervallo di tempo t= 2 π / ω (tempo impiegato per generare una sinusoide, si osserva immediatamente che la potenza dissipata è sempre positiva e varia nel tempo con una legge cosinusoidale.
Infatti (applicando in modo opportuno le leggi della bisezione) abbiamo:
W= Io 2 R sen 2ω t:= Io 2 R (1-cos 2 ω t:)/2
che rappresentata da due cosinusoidi traslate in (0; I2 R/2)
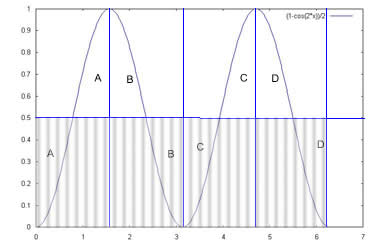
Si osserva che su un periodo L'area della cosinusoide è equivalente all'area di un rettangolo di altezza: Io 2 R/2 e questa è la potenza media.
Confrontando la potenza media ricavata con la formula della potenza determinata per la corrente alternata ricaviamo:
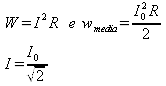
Ossia la corrente alternata dal punto di vista della legge di Ohm si comporta come una corrente continua di intensità I=Io / √ 2
Facendo lo stesso ragionamento ricaviamo per il potenziale variabile :
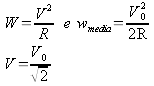
Ossia la corrente alternata dal punto di vista della legge di Ohm si comporta come una corrente continua con una forza elettromotrice V=Vo / √ 2.
Pertanto nei circuiti ohmici, per la dissipazione termica, la corrente alternata si comporta come la corrente continua.
Se consideriamo circuiti diversi da quelli ora cosa accadrà?
Studieremo i circuiti RC (resistivo capacitico) e i circuiti RL (resistivo induttivo).
Nei circuiti ohmici pertanto possiamo scrivere
Cosa accade se prendiamo in considerazione un circuito contenente una resistenza e un induttore (un solenoide) in serie oppure un induttore e un condensatore?
Si ricava che il comportamento non è assimilabile a quanto previsto debba valere nei circuiti a corrente continua.
Prendiamo ad esempio in considerazione un circuito RCL come in figura:
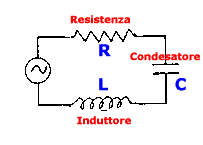
In questo circuito sia il condensatore C che l'induttore L contribuiscono come generatori sfasati di corrente alternata. Per questi circuiti dobbiamo scrivere:
V=Z I (dove Z prende il nome di impedenza).
Per il circuito RCL: