Consideriamo un contenitore a forma
cubica contenente un gas ideale. Consideriamo una molecola che
urta una parete perpendicolare all'asse delle ascisse.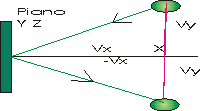
Considerando l'urto elastico tra la molecola e la parete si osserva che le componenti y e z della velocità non si modificano solo Vx diventa -Vx e quindi Δ V = -2 Vx
quindi δ p = -2mVx e quindi l'impulso F'Δt = Δ p
Pertanto la forza trasmessa dalla parete alla molecola sarà F' = -2mVx / Δt.
Per la 3° legge della dinamica la forza trasmessa alla parete sarà F=-F' e quindi F = 2mVx / Δt.
Per determinare Δt è opportuno considerare la forza media trasmessa alla parete tra due urti successivi e Δt non è altro che l'intervallo di tempo che passa tra un urto e il successivo. Non considerando le componenti y e z (ininfluenti nella nostra analisi) Vx = Δ X / Δ t
ΔX= 2 L ( andata e ritorno = L + L) e quindi
Δ t = ΔX/Vx
Δ t =2 L /Vx
Fmedia = 2mV2x / 2 L = mV2x / L
Questa è la forza trasmessa da una delle molecole sulla parete.
La F media trasmessa da tutte le molecole sulla parete è pari alla somma di tutte le forze quindi:
Fmedia totale = Σ mV2x / L
Se consideriamo l'energia cinetica media posseduta da tutte le molecole contenute nel recipiente avremo
E cinetica media tot. = Σ 1/2 m (V2x +V2y +V2z ) ossia
E cinetica media tot. = 1/2 m (ΣV2x +ΣV2y +ΣV2z )
Non esistendo direzioni privilegiate possiamo imporre che mediamente ΣV2x = ΣV2y = ΣV2z =
ossia Vmedia2 = 3 ΣV2x /N (N è il numero di molecole presenti nel recipiente)
E cinetica media di 1 molecola = 3/2 m V2media /N e quindi
ΣmV2x = 2/3 N E cinetica media di 1 molecola = 2/3E cinetica del gas .
Pressione = F / Sup = F / L2 ( base quadrata)
Fmedia totale = Σ mV2x / L
Pressione = Fmedia totale /L2 = 2/3 E cinetica del gas /L3 ( volume del cubo)
P V = 2/3 E cinetica del gas
ma per i gas ideali P V=n R T
E cinetica del gas = 3/2 n R T
Nei gas perfetti l'energia cinetica è direttamente proporzionale alla temperatura!