DEFINIZIONE:

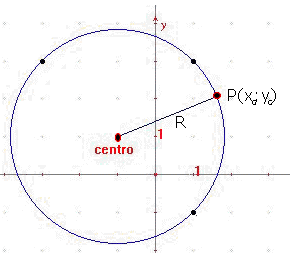La circonferenza è il luogo geometrico dei punti del piano equidistanti da un punto fisso chiamato centro.

Partendo dalla definizione di luogo geometrico ricaviamo:

(x-x_c)²+(y-y_c)²= R²

Sviluppando i quadrati e sistemando i termini otteniamo:

x²+y²+ax+by+c=0

con:

a=-2x_c
b=-2y_c
c=x_c²+y_c²-R²

per ricavare l'equazione della circonferenza determinando
i valori di: a - b - c

Passaggio per punto assegnato	Sostituire nell'equazione generica alle variabili x e y i valori delle corrispondenti coordinate. Si ottiene un'equazione nei tre parametri a,b,c.
Centro assegnato	Si ottengono 2 condizioni: a=-2xc b=-2yc
Diametro assegnato (gli estremi)	Si ottengono 3 condizioni: Si determina il centro quale punto medio degli estremi. Si determina il raggio (distanza centro - uno degli estremi).
retta a cui appartiene il centro	1 Condizione: Se ad esempio il centro appartiene alla retta 2x+3y-1=0 ricaviamo la condizione da sfruttare nel sistema sostitundo alla x della retta -a/2 e alla y della retta -b/2 ottenendo: 2(-a/2)+3(-b/2) -1=0 e quindi fatti i calcoli 2a+3b+2=0

Tre parametri - tre condizioni.

Mettere a sistema le tre equazioni ricavate e determinare i valori dei tre parametri.

Caso particolare

Se conosciamo le coordinate del centro e il valore del raggio possiamo utilizzare l'equazione in forma implicita e sostituire i valori noti alle coordinate del centro e a R il suo valore.

Circonferenza-retta

Valgono sempre le considerazioni viste per la parabola.

Ricordarsi che è sempre possibile sfruttare quanto già studiato nei primi anni e sopratutto che:

Se una retta è tangente ad una circonferenza la sua distanza dal centro è uguale al raggio.

Ricordarsi inoltre che il raggio nel punto di tangenza è sempre perpendicolare alla tangente.