Prima di iniziare a parlare di algoritmo è opportuno fare una breve digressione sul concetto di modello e un breve excursus sulla logica matematica.
Come e perché costruire un modello.
Per capire cosa implichi il concetto di modellizzazione iniziamo con un esempio.
Supponiamo che ad un elettricista e ad un arredatore venga richiesta la ristrutturazione di un locale.
Ambedue opereranno sullo stesso ambiente, ma saranno costretti ad utilizzare in modo diversificato le informazioni fornite.
È evidente che ciascuno tratterrà e sfrutterà solo alcune
delle notizie comunicategli.
L'elettricista realizzerà un modello della stanza in cui saranno riportate
le posizioni dei pilastri, dei cavi elettrici già presenti, le posizioni dei tubi
dell'acqua e del gas,...
ossia di tutto che deve conoscere prima di realizzare l'impianto elettrico
L'arredatore invece realizzerà un modello di stanza nel quale verranno riportate
le posizioni delle finestre, quelle delle porte, l'esposizione della stanza,
nonché la destinazione della stessa.
L'oggetto analizzato è sempre lo stesso anche se ognuno estrarrà di tutto
solo ciò che interessa avendo presente quello che dovrà successivamente
realizzare.
Possiamo quindi definire MODELLIZZAZIONE
Quando dobbiamo dimostrare un teorema leggiamo il testo e quindi prima di effettuare la dimostrazione effettuiamo una modellizzazione sia scrivendo nelle ipotesi solo le informazioni che successivamente utilizzeremo sia concentrandoci unicamente su un determinato insieme di teoremi precedentemente dimostrati, che pensiamo ci potranno servire nella successiva dimostrazione. In ogni caso dobbiamo essere in grado di ottenere tutte le informazioni essenziali eliminando eventualmente quelle superflue.
Attualmente l'ente con cui dobbiamo confrontarci è un computer, una macchina aspecifica collegato a varie periferiche ( monitor, tastiera, hard disk, ...) in grado di eseguire solo determinate serie di azioni. Sarebbe assurdo chiedere ad un personal di ballare un valzer o di fare un caffè (a meno che non venga inserito o in un robot o in una macchina in grado di fare un caffè) e pertanto dobbiamo sempre aver presente quali sono le prestazioni ottenibili da detta macchina. Un elaboratore elettronico può essere usato per gestire archivi, effettuare calcoli, simulare comportamenti, realizzare giochi iterativi, rappresentare diagrammi, ...
E' evidente che un computer per poter eseguire ciò che gli viene richiesto deve essere preventivamente correttamente istruito.
Chiameremo programma l'insieme delle istruzioni impartite.
Ogni istruzione deve essere impartita in linguaggio macchina (espresso da un numero binario compreso tra 00000000 e 11111111), fortunatamente oggi esistono "compilatori" ossia programmi che trasformano le istruzioni impartite in inglese in istruzioni in linguaggio macchina.
Per redigere un algoritmo risolutivo dobbiamo determinare quali grandezze dovremo utilizzare e come vorremo utilizzare le stesse.
Chiameremo dato ogni grandezza che dovremo utilizzare per redigere l'algoritmo risolutivo.
Ogni dato sarà associato ad un nome, un'etichetta che identificherà senza alcuna ambiguità il valore della grandezza associata.
Dati
- Costanti (valore invariabile all'interno dell'algoritmo);
- Variabili scalari: "nome, valore"
- Variabili vettoriali: "nome, insieme di valori"
(il valore delle variabili è indeterminato all'inizio di un algoritmo).
Successivamente elencheremo le istruzioni, che dovranno essere:
- Istruzioni operative (producono risultati se eseguite);
- Istruzioni di controllo (in funzione del verificarsi di condizioni determinano l'esecuzione di alcune istruzioni piuttosto che di altre);
- Istruzioni di salto (alterano l'ordine di esecuzione delle istruzioni);
- Istruzioni di inizio e fine;
- Istruzioni di trasmissione dati o messaggi fra l'ambiente esterno e l'algoritmo.
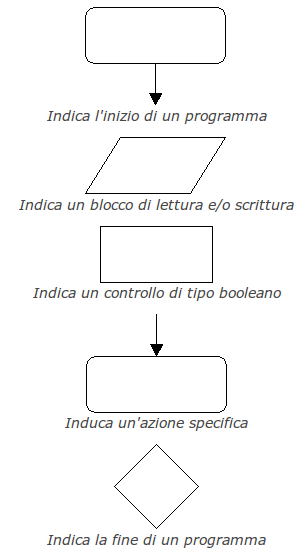
Per rappresentare la sequenza delle istruzioni utilizzeremo dei simboli che associeremo ai diagrammi di flusso.
Ecco un esempio di blocchi e loro significato.
Consideriamo un problema e il relativo diagramma di flusso.
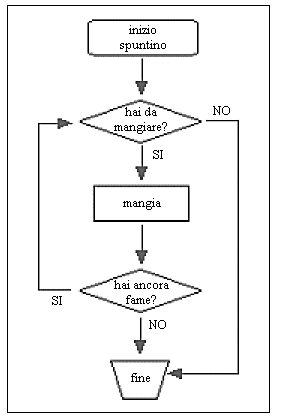
Prendiamo in esame un semplice ragionamento che verifica se è possibile fare uno spuntino,
tale programma viene spiegato come segue:
- Inizia lo spuntino
- Hai a disposizione qualcosa da mangiare?
- Mangia
- Hai ancora fame?
- Fine dello spuntino
Esposto in questo modo l'algoritmo risulta di difficile comprensione, ma rappresentandolo con un diagramma di flusso possiamo comprendere l'esatto funzionamento del ragionamento.
In questo contesto il rombo rappresenta l'istruzione condizionale legata ad una scelta.