Proposte esercizi da svolgere

Integrali

...

Integrali indefiniti

$\displaystyle \int$ x ² d x , $\displaystyle \int$ cos x d x , $\displaystyle \int$ 3 x ²- 2 sin x d x $\displaystyle \int$ x 2 x d x

$\displaystyle \int$ 4 x ³- 3 x ²+ 1 d x , $\displaystyle \int$ 3 sin x - 2 cos x d x , $\displaystyle \int$ 2 e ^x d x , $\displaystyle \int$ $\displaystyle {\frac{2 dx}{x}}$

$\displaystyle \int_{0}^{1}$ x ²+ x d x , $\displaystyle \int_{0}^{\pi}$ 2 sin x - cos x d x , $\displaystyle \int_{-1}^{1}$ 3 e ^x- x d x

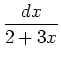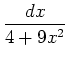
$\displaystyle \int$ cos(2 x + 3) d x , $\displaystyle \int$ e ^{3x - 4} d x , $\displaystyle \int$ $\displaystyle {\frac{dx}{2+3x}}$ , ; $\displaystyle \int$ $\displaystyle {\frac{dx}{4 + 9x^2}}$

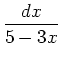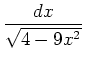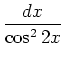$\displaystyle \int$ $\displaystyle {\frac{dx}{5-3x}}$ , $\displaystyle \int$ $\displaystyle {\frac{dx}{\sqrt{4 - 9x^2}}}$ , $\displaystyle \int$ $\displaystyle {\frac{dx}{\cos^2 2x}}$ , $\displaystyle \int$ $\displaystyle {\frac{dx}{e^x}}$

Integrali definiti

$\displaystyle \int_{0}^{1}$ x ³ d x , $\displaystyle \int_{-2}^{3}$ ( x ²- 3 x + 1) d x , $\displaystyle \int_{0}^{\pi}$ sin(2 x) d x , $\displaystyle \int_{2}^{4}$ $\displaystyle {\frac{dx}{x}}$

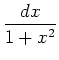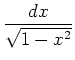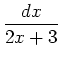
$\displaystyle \int_{0}^{1}$ $\displaystyle {\frac{dx}{1+x^2}}$ , $\displaystyle \int_{0}^{1/2}$ $\displaystyle {\frac{dx}{\sqrt{1-x^2}}}$ , $\displaystyle \int_{1}^{2}$ dx e^{x/2 ,} $\displaystyle \int_{1}^{4}$ $\displaystyle {\frac{dx}{2x+3}}$

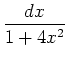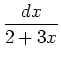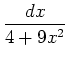
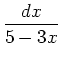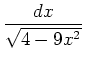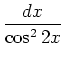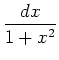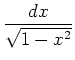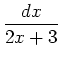
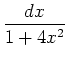$\displaystyle \int_{0}^{\infty}$ e ^-2x d x , $\displaystyle \int_{0}^{\infty}$ $\displaystyle {\frac{dx}{1+4x^2}}$ , $\displaystyle \int_{1}^{x}$ $\displaystyle {\frac{dt}{t}}$ , ( x > 0)

$\displaystyle \int_{-a}^{a}$ (3 x ⁷- 4 x 5) ¹⁵ d x , $\displaystyle \int_{0}^{\pi/4}$ sec ²x d x , $\displaystyle \int_{1}^{e^{x^2}}$ $\displaystyle {\frac{du}{u}}$ .

Christopher Kent Mineman - Didattica in rete

Integrali