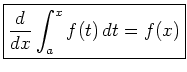Christopher Kent Mineman - Didattica in rete

Consideriamo l' intervallo [ a , b ]. Sia f (x) una funzione continua definita su questo intervallo.

Pensiamo  di voler calcolare la superficie della zona sotto il grafico della f (x) fra x = a e x = b .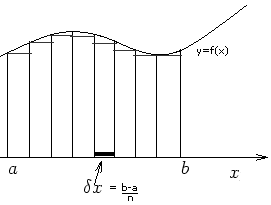

Per risolvere il problema adotteremo un metodo molto elementare. Dividiamo l'intervallo [ a , b ] in in "n" parti ciascuna di ampiezza dx = (b-a)/n. Per convenienza le prenderemo tutte della stessa larghezza, ma questa scelta è ininfluente per la definizione che vogliamo dare. Con questa suddivisione determiniamo "n" strisce sottili come in figura.

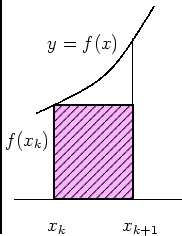
Per calcolare la superficie per diffetto costruiamo n rettangoli scegliendo per altezza l'ordinata minore di ogni striscia.

Il rettangolo sulla base [ x K , x K + 1 ] ha per superficie f ( x k) δ x . Così l'area complessiva della figura mistilinea è maggiore della somma delle aree degli n rettangoli così individuati

Superficieinferiore >  $\displaystyle \sum_{k=0}^{n-1}$  f( x k_min) δx

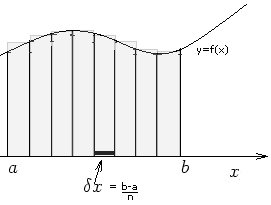
Per calcolare la superficie per eccesso costruiamo n rettangoli scegliendo per altezza l'ordinata massima di ogni striscia.

Il rettangolo sulla base [ x K , x K + 1 ] ha per superficie f ( x k_max) d x . Così l'area complessiva della figura mistilinea è maggiore della somma delle aree degli n rettangoli così individuati

Superficiesuperiore >  $\displaystyle \sum_{k=0}^{n-1}$  f( x k_max) δx

Ora usiamo lo stesso genere di argomento che è stato utilizzato quando si è definito il concetto di derivata.

Se incrementiamo il numero di suddivisioni diminuisce sempre di più la differenza tra la Superficiesuperiore e la Superficieinferiore

È intuitivo ipotizzare che la differenza sarà uguale a zero ossia Superficiesuperiore= Superficieinferiore se prendessimo il limite per n che $ \to$$ \infty$.

Così la superficie del trapezio mistilineo sarà = $\displaystyle \lim_{n\to\infty}^{}$$\displaystyle \sum_{k=0}^{n-1}$ f ( x k) δ x

Ma già sappiamo che questa zona è data dall'integrale definito. Così, unendo i nostri due risultati, otteniamo (nel caso d'una funzione continua)

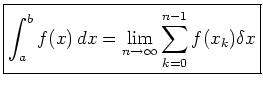
$\displaystyle \boxed{\int_a^b f(x) dx = \lim_{n\to\infty} \sum_{k=0}^{n-1} f(x_k)\delta x }$

Possiamo in effetti prendere questo come definizione dell' integrale definito (l' integrale di Riemann) e normalmente facciamo in modo da nel lavoro più avanzato. Questa interpretazione dell' integrale definito è quella che è la più utile nelle applicazioni, come presto vedremo.

Il teorema fondamentale

Data la funzione y=f(x) continua in [a;b], esiste la funzione integrale F(x),. Tale funzione è derivabile in tutto [a;b] e risulta F'(x)=f(x).

Dimostrazione

Dimostriamo innanzitutto che F(x) è una funzione. Qualsiasi sia il punto scelto, l'integrale tra a e x esiste ed è unico il numero definibile con la tecnica sovra esposta. Inoltre è una funzione continua, incrementandosi con continuità l'area all'incrementare vel valore assunto dalla x. Pertanto essendo una funzione continua possiamo calcolare la sua derivata in ogni punto dell'intervallo [a;b].

Siano x e x+ due punti qualsiasi appartenenti all'intervallo [a;b]. Calcoliamo il rapporto incrementale:

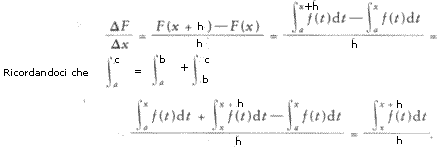
Pe il teorema della media, l'integrale della funzione è sempre equivalente all'area di un rettangolo di base h e altezza f(c) essendo c una 'x' compresa tra x e x+h.

Pertanto possiamo scrivere: 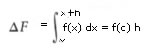e quindi

Anche passando al limite per h tendente a zero il rapporto incrementale vale f(c) è 'c' che tende inesorabilmente a 'x' essendo x<c<x+h.

Pertanto avremo:

Considerazioni

Il collegamento fra i due concetti di base, la derivata e l' integrale, è forse la caratteristica più importante del calcolo. Questo collegamento può essere ricapitolato approssimativamente dicendo che l' integrazione e la differenziazione sono funzioni inverse l'una dell'altra.

Per descrivere più precisamente quanto detto, deve essere introdotto il concetto dell'integrale indefinito. Supponendo che la f (x) sia continua (quindi, integrabile) in un certo intervallo I e siano a e X due punti di questo intervallo. Se il numero a è fisso, quindi una funzione di X, la F (X), può essere definita come l'integrale della f(x) da 'a' a 'X' ; se X < a, la F (X) è uguale all'opposto dell' integrale da X alla a . La funzione la F (X) è chiamata un integrale indefinito della funzione la f (x).

Il collegamento fra derivata ed integrale può allora essere ricavato nel modo seguente: la funzione la F (X) (come definito sopra) è differenziabile e F ' (X) = f (X); ancora, se la G (X) è qualunque altra funzione differenziabile che soddisfa la relazione G ' (X) = la f (X) per ogni X appartenente all'insieme I , quindi la differenza F (X) - G (X) è costante.

RIASSUMENDO:

sia g (x) = $\displaystyle \int_{a}^{x}$ f (t)   d t    dove la a è un costante e stiamo pensando al limite superiore dell' integrale come variabile.

Se la F (x) allora è un integrale indefinito per la f (x) allora g (x) = F (x) - F ( a )

Così, tramite la definizione della F (x),

g ' (x) = F ' (x) = f (x)

Ciò fornisce il risultato
$\displaystyle \boxed{ \frac{d}{dx}\int_a^x f(t) dt = f(x) }$
(n.b.: la abbiamo dimostrata soltanto sul presupposto che un integrale indefinito esista per la f (x).)