Abbiamo visto che cosa significhiamo da un integrale definito dove entrambi i limiti di integrazione sono limitati . In molte applicazioni importanti di integrazione verrete attraverso i casi dove uno o più dei limiti di integrazione è infinito. Ci sono tre possibilità:
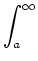 f(x)dx oppure
f(x)dx oppure 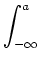 f(x)dx
oppure
f(x)dx
oppure 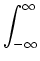 f(x)dx
f(x)dx
L' interpretazione di questi è che devono essere prese come casi di limite degli integrali corrispondenti con gli estremi limitati. Per esempio,
Naturalmente, nella maggior parte dei casi i limiti non esisteranno, in tale caso neanche anche l' integrale esisterà. Per esempio,
Consideriamo ora questo integrale generalizzato: