Christopher Kent Mineman - Didattica in rete

SOLIDI DI ROTAZIONE

Consideriamo il grafico di y = f (x) nell' intervallo [ a , b ] e ruotarlo attorno all'asse x in modo da ottenere il solido di rotazione come indicato nella figura. Come calcolare  il volume di questo solido?

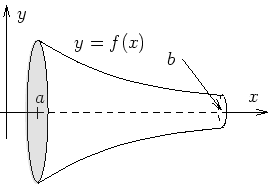
integrali solidi di rotazione

Suddividere l' intervallo [ a , b ]  in n (con n estremamente grande) parti di lunghezza dx e considerare gli infiniti cilindri di raggio f(x) e altezza dx.

Il volume d'una sezione infinitesima
\psfrag{y}{$y$}\psfrag{dx}{$\delta x$}\includegraphics[width=3cm]{../xfig/slice-volume.eps}

Nella notazione dello schema, la fetta sottile del solido è virtualmente un cilindro del raggio f(x) e di spessore dx . Il volume d'un cilindro è il prodotto della relativa altezza e della zona della relativa base. Così otteniamo l' approssimazione d V = [f(x)] 2  d x per il volume della sezione infinitesima.

L' approssimazione al volume totale può allora essere scritta come (Y = f(x) )

V ≈ Σ π y 2  d x
Ora calcoliamo il volume passando al limite di n → ∞
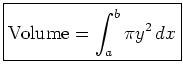
$\displaystyle \boxed{ \text{Volume} = \int_a^b \pi y^2 dx }$

Sfera

Presa il semicerchio delimitato dalla semicirconferenza y = $ \sqrt{r^2-x^2}$ nell'intervallo [ - r , r ] e fatta una rotazione di 360º attorno all'asse x. Otteniamo, come  solido di rotazione, una sfera di raggio r .

La nostra formula ci dice che il volume di questa sfera sarà e calcoliamo l'integrale associato:

V = $\displaystyle \int_{-r}^{r}$$\displaystyle \pi$ ( r 2 - x 2)   d x = $\displaystyle \left[\vphantom{ \pi r^2x - \frac{1}{3}\pi x^3}\right.$$\displaystyle \pi$ r 2 x - $\displaystyle {\textstyle\frac{1}{3}}$$\displaystyle \pi$ x 3 $\displaystyle \left.\vphantom{ \pi r^2x - \frac{1}{3}\pi x^3}\right]_{-r}^{r}$ = $\displaystyle {\textstyle\frac{4}{3}}$$\displaystyle \pi$ r 3

Così il volume d'una sfera del raggio r è

V = $\displaystyle {\textstyle\frac{4}{3}}$$\displaystyle \pi$ r 3

Un altro esempio   

Considerato l' imbuto costituito dalla presa della curva y = 1 / x e dalla rotazione esso intorno all'asse x nell' intervallo [ 1, a ], come indicato nella figura

Volume di rotazione.
\psfrag{1}{$1$}\psfrag{a}{$a$}\includegraphics[width=6cm]{xfig/one-over-x.eps}

Il volume di questo imbuto è

V = $\displaystyle \int_{1}^{a}$$\displaystyle \pi$$\displaystyle {\frac{1}{x^2}}$  d x = -$\displaystyle \left[\vphantom{-\frac{\pi}{x}}\right.$$\displaystyle {\frac{\pi}{x}}$$\displaystyle \left.\vphantom{-\frac{\pi}{x}}\right]_{1}^{a}$ = $\displaystyle \pi$ (1 - $\displaystyle {\frac{1}{a}}$)

Ora notare che, se a $ \to$$ \infty$, questo volume tende a $ \pi$

Scriviamo

$\displaystyle \int_{1}^{\infty}$$\displaystyle {\frac{\pi}{x^2}}$  d x = $\displaystyle \lim_{a\to\infty}^{}$$\displaystyle \int_{1}^{a}$$\displaystyle {\frac{\pi}{x^2}}$  d x = - $\displaystyle {\frac{\pi}{a}}$$\displaystyle \left.\vphantom{ \pi-\frac{\pi}{a}}\right)$ = $\displaystyle \pi$