Keplero
Keplero, allievo di Tycho Brahe, avendo a disposizione i dati del suo maestro
ed usandoli correttamente, creò un modello eliocentrico che, però,
non riusciva a completarsi nel suo insieme.
Per migliorarlo e renderlo perfetto egli provò a cambiare i dati del
suo maestro supponendo che LE TRAIETTORIE DELLE ORBITE NON FOSSERO CIRCONFERENZE
ma ELLISSI.
Questa fu la scelta vincente. Ripercorrendo i suoi studi con questa variazione
Keplero riassunse i suoi risultati, validi per tutti i pianeti , in 3 leggi:
1 legge:
Tutti i pianeti ruotano attorno al sole seguendo orbite ellittiche che hanno
un fuoco in comune occupato dal Sole.
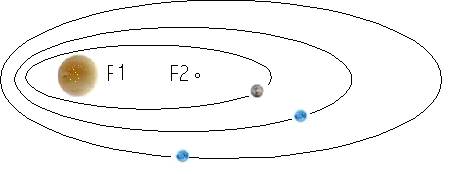
Il Sole è posto su uno dei due fuochi.
Questa legge distruggeva il concetto di moto perfetto: quello circolare con
velocità costante.
ELLISSE: è il luogo geometrico dei punti del piano la cui somma delle distanze da due punti fissi (fuochi) è costante.
|
2 legge:
La velocità AREOLARE è costante: i tempi impiegati a descrivere
aree uguali sono uguali.
Per AREA si intende la superficie descritta dal segmento che congiunge il
pianta al sole nel tempo.
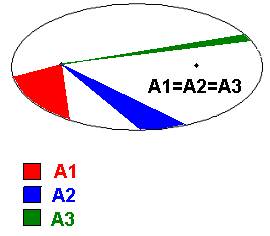
Se le due aree sono uguali allora il tempo impiegato è uguale, però nella prima area si muove a velocità maggiore perché ha più strada da percorrere.
3 legge
Detta R la distanza media Sole-Pianeta, il cubo di tale distanza è proporzionale al quadrato del periodo T di rivoluzione.
R3 = K x T2
K= costante che vale 3,38 x 1018 m3/sec2
T= tempo di rivoluzione per descrivere un orbita completa
R= Distanza media dal sole.
Attenzione:
Le prime due leggi valgono sempre sia per i pianeti attorno al sole che per
i satelliti attorno alla terra.
La terza legge vale solo se si effettua la seguente correzione:
Quindi:
R3
--- = K0 x Mcentrale
T2
Keplero ha studiato la cinematica dell'Universo usando queste leggi che valgono
anche per l'Universo.
Quindi: il Sole e i pianeti si muovono nell'Universo seguendo le stesse leggi.
NEWTON e la gravitazione universale
NEWTON e la forza di gravitazione universale
Con Keplero il modello eliocentrico poteva definirsi affermato. Però
dal punto di vista fisico rimanevano irrisolti 2 quesiti fondamentali:
Perché i pianeti si muovono così?
Qual è la forza che lega i pianeti al sole?
Per rispondere a questi due quesiti Newton determinò la legge di gravità universale.
La dimostrazione che facciamo considera un caso particolare: Pianeta che ruota attorno al Sole su una traiettoria circolare di moto circolare uniforme.
Per l'equilibrio dobbamo porre la condizione che la forza centripeta (che chiameremo Forza di gravitazione) sia uguale alla reazione vincolare ossia alla forza centrifuga dovuta al moto circolare uniforme.
Fcentripeta= m R w2
con m = massa del pianeta.
w = 2 p / T
Fcentripeta= mR(2 p / T)2 = mR(2 p)2 1/ T2
Ma dalla terza legge di Keplero
R3
--- = K0 x Mcentrale
T2
ossia:
1/ T2= K0 x Mcentrale/R3
Fcentripeta=mR(2 p / T)2=m(2 p)2RK0xMcentrale/R3
Fcentripeta= [(2 p)2 K0] x m Mcentrale/R2
Definiamo G = [(2 p)2 K0]
G = 6,67 x 10-11
… quindi…
Fgravitazione universale= [(2 p)2 K0] x m Mcentrale/R2