Il lavoro, che è il prodotto scalare della Forza per lo spostamento.
E' un particolare prodotto tra vettori il cui risultato è uno scalare ossia un numero reale.
La nuova grandezza che associamo al lavoro è l'energia.
Se il lavoro è positivo il corpo acquista energia, mentre se è negativo il corpo perde energia.
Per determinare il lavoro possiamo utilizzare due strumenti matematici.
Se la forza e lo spostamento vengono visualizzati come segmenti orientati scriveremo:
L = F s cos a
Se la forza e lo spostamento vengono espressi in coordinate vettoriali: F(Fx;Fy;Fz) e S(Sx;Sy;Sz) il lavoro verrà determinato da:
L=FxSx+FySy+FzSz
Per trovare il lavoro di una forza, consideriamo quattro casi particolari:
| L = F·s | |
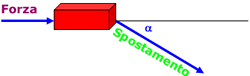 |
L = F·s·cos α |
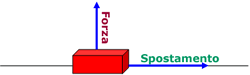 |
L=0 |
| L=-F.S |
Energia Cinetica
Un corpo di massa m e velocità v è dotato di energia, detta energia cinetica per il fatto di essere associata al moto.
Tale energia è espressa dalla relazione
Ec = ½·m(massa)·v2(velocità)
Un altro modo di scrivere la formula per calcolare l’energia cinetica
è…
Ec = P2(quantità di moto)/2m
…poiché
½·m·v2 = m2·v2/2m
= P2/2m
In quanto P = m·v
…e quindi m2·v2=P2
L’energia cinetica di un corpo è associata al lavoro
della forza F dalla seguente relazione L= ΔEc
Questa formula è stata dedotta a partire dalle leggi della dinamica e pertanto la correttezza di quelle leggi comporta la sua correttezza.
Per la dimostrazione partiamo dall'analisi di un corpo sottoposto all'azione di una forza costante e che si muove nella direzione coincidente con la direzione della forza con velocità iniziale vi.
Nel moto rettilineo uniformemente accelerato abbiamo
a=(v2 -vi)/t
L = F•s = m•a•s
Dalle leggi della cinematica:
x-x0 = ½at2 + vit e quindi
x-x0 =½[(v2-vi)/t] t2 + vit
x-x0 =½[(v2 • vi)] t + vit
x -x0 =½[<(v2 +vi)] t
Pertanto il lavoro
L = [m•(v2 -v1)]/t•½t(v2 + v1)=½m (v22 - v12)
L =½mv22- ½mv12
La formula contiene variabili che dipendono solo dalla velocità finale e dalla velocità iniziale. Non ci sono mezzo velocità intermadie e non cioé velocità prima che la forza cominciasse a spingere. La grandezza che dipende solo da una massa e da una velocità, la chiamiamo Energia Cinetica.
Quindi Lavoro = Ecf-Eci(teorema delle forze vive)
Problemi
1°
1. Un missile di massa 80 kg sta viaggiando negli spazi interplanetari
verso la destra di un osservatore O con una velocità di 300 m/sec.
A un certo istante esplode in due frammenti, uno di 50 kg e uno di 30
kg. L’osservatore O valuta ora che il primo dei due spezzoni viaggia
verso la sua sinistra con la velocità di 200 m/sec. In base a
questo dato determinare la velocità del secondo spezzone, sempre
rispetto all’osservatore O.
Prima Dopo
massa=80 kg m1=30 kg m2=50 kg
velocità=(300;0) v1=(-200;0) v2=(vx;vy)
P=m·v
| Pprima | = Pdopo |
| 80(300;0) | =30(-200;0)+50(vx;vy) |
| (24000;0) | =(-6000;0)+(50vx;50vy) |
| (24000;0) | =(50vx-6000;50vy+0) |
Risolvendo per componenti:
50vx-6000 =24000
50vx=30000
vx=600
50vy+0=0
50vy=0
vy=0
v2 =(600;0)=600 m/sec lungo l'asse x
2°
2. Un oggetto di massa 200 kg si disintegra in due parti; una parte, di massa
50 kg, si sposta verso sinistra su una retta che forma un angolo di 30°
con l’asse x ad una velocità di 400 m/sec. Sapendo che l’oggetto
all’inizio è fermo, calcolare la velocità a cui viaggia
dopo.
| Prima | Dopo |
| massa=200kg | m1=50 kg m2=150 kg |
| velocità=(0;0) | v1=(-346;200) v2=(vx;vy) |
|
Pprima |
=Pdopo |
| (0;0) | =m1·v1+m2·v2 |
| (0;0) | =50(-346;200)+150(vx;vy) |
| (0;0) | =(-17300;10000)+(150vx;150vy) |
| (0;0) | =(150vx-17300)+(150vy+10000) |
150vx-17300=0
vx=115
150vy+10000=0
vy=-66
v2=(115;-66)=
|v|=(1152+662)1/2=133 m/sec