Enunciato:
La somma degli inversi delle distanze tra il vertice dello specchio e
un oggetto posto sul suo asse ottico e la distanza tra il vertice e l'immagine
coniugata è equivalente all'inverso della distanza del fuoco dal
vertice dello specchio.
DIMOSTRAZIONE
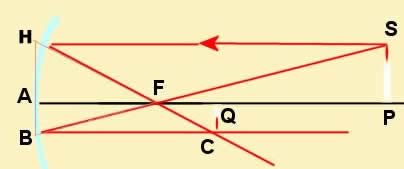
| Poniamo: | AP = p | AQ = q | AF = f |
Nella dimostrazione supponiamo che in prima approssimazione la superficie
concava possa essere approssimata ad una superficie piana.
L'ingrandimento è dato da:
| G= | QC SP |
ossia rapporto tra le dimensioni dell'immagine e quelle dell'oggetto
originale.
Consideriamo i triangoli AHF e FQC,che sono simili (tre angoli uguali)
e quindi hanno i lati in proporzione.
Allora G = QC / AH (essendo AH = SP) e per la similitudine
QC
AH |
= |
FQ
AF |
= |
q-f
f |
Consideriamo i triangoli SPF e AFB, che sono simili (tre angoli uguali)
e quindi hanno i lati in proporzione.
Allora G = AB / FP (essendo AB = QC) e per la similitudine
AB
FP |
= |
AF
FP |
= |
f
p-f |
Uguagliando quindi gli ingrandimenti si ottiene:
f
p-f |
= |
q-f
f |
Svolgendo i calcoli si ottiene:
f2 = pq–fq–fp+f2
e semplificando:pq = fq+fp
Dividendo ogni termine per fpq si ottiene:pq
fpq |
= | fq
fpq |
+ | fp
fpq |
Quindi:
1
f |
= |
1
p |
+ |
1
p |