Essendo
ci
si rende conto che per utilizzare proficuamente la relatività
speciale dobbiamo introdurre un nuovo concetto, quello di EVENTO.
L'evento è qualsiasi fatto accaduto in un punto e in un certo istante.
L'evento è l'equivalente del paletto messo dall'agrimensore per fissare la posizione di un punto in un campo.
Due eventi determinano un intervallo spazio-temporale, come due paletti fissano la lunghezza del segmento avente per estremi i punti in cui sono infilati i due paletti.
Se i paletti
pòossono essere posti in un piano cartesiano tridimensionale
di coordinate P1(x1;y1;z1)
e P2(x2;y2;z2) la distanza
tra i due punti sarà data da: 
(teorema
di Pitagora applicato al parallelepipedo).
La distanza nello spazio ordinario è assimilabile ad una ipotenusa (somma dei quadrati...).
N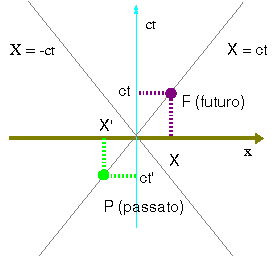
ello
spazio-tempo relativistico abbiamo la differenza perchè l'intervallo
è un cateto (la distanza temporale funge da ipotenusa e quella
spaziale da cateto), come si evince dalla dimostrazione.
Per calcolare distanze tra eventi dobbiamo colstruire un piano cartesiano quadridimensionale (difficile da realizzare!).
Per semplificare tale costruzione immaginiamo di poter rappresentare tutto in uno spazio bidimensionale, associando la dimensione c t all'asse delle ordinate e x all'asse delle ascisse, immaginando di operare in uno spazio monodimensionale.
Le rette X=ct rappresentano i punti evento associati ad un impulso luminoso che passa nell'istante t=0 per il punto X=0.
F rappresenta l'evento in cui la luce ha raggiunto il punto X (nel futuro).
P rappresenta l'evento in cui la luce ha raggiunto il punto X' (nel passato) prima di raggiungere l'origine.
Essendo 
una distanza possiamo operare in modo che l'unità di misura sull'asse
dei tempi sia il metri (metri temporali) se effettuiamo un cambio di
variabile ponendo t=ct', la nuova grandezza sarà una lunghezza
che coincide con t' solo se ridimensioniamo il sistema in modo che c
valga 1.
1 metro di tempo
è pari a |
1
c |
secondi |
Ossia 10-9secondi=0,299792458 metri di tempo
1 metro di tempo= 3,33564 nanosecondi.
Utilizzando questa nuova unità di misura l'intervallo può essere scritto:
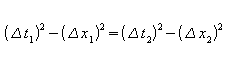
con le distanze temporali e spaziali tutte espresse in metri.
Un evento è associato alla conoscenza di una posizione ed un istante temporale.
Per descrivere quanto rilevato siamo portati a definire uno spazio a 4 dimensioni:
- Tempo
- coordinata x
- coordinata y
- coordinata z
Nello spazio ordinario il modulo di un vettore differenza ΔV( Δx; Δy; Δz) è dato da: | ΔV|²= (ΔX)²+ (ΔY)²+ (ΔZ)²
mentre nel caso dello spazio-tempo il modulo dell'evento spazio-temporale è dato da (Δ τ)²=(Δt)² -(ΔX)²-(ΔY)²-(ΔZ)²
Per riportarci allo spazio ordinario dobbiamo imporre che le coordinate spazioali siano immaginarie rispetto a quelle temporali ( ricordiamoci che i²=-1) e quindi un punto nello spazio-tempo sarà associato ad in vettore di coordinate (t,ix;iy;iz).