Uno dei fenomeni più sconcertanti studiati verso la fine del secolo
scorso fu la distribuzione spettrale della radiazione del corpo nero.
Un corpo nero è un sistema ideale che assorbe tutta la radiazione
che incide su di esso; esso può essere approssimato da una cavità
con una piccolissima apertura, com'è illustrato nellla figura
Le caratteristiche della radiazione in una tale cavità di un corpo dipendono
solo dalla temperatura delle pareti. A temperature ordinarie (sotto 600°C),
la radiazione termica emessa da un corpo nero non è visibile, perché
l'energia è concentrata nella regione infrarossa dello spettro elettromagnetico.
Se si riscalda il corpo, la quantità di energia irraggiata aumenta
(secondo la legge di Stefan-Boltzmann, ) e la concentrazione di energia si
sposta a lunghezze d'onda minori. Tra circa 600 °C e 700 °C c'è
abbastanza energia nello spettro visibile da far sì che il corpo emetta
una luce di colore rosso scuro; a temperature più alte esso diventa
rosso brillante o addirittura «incandescente».
La figura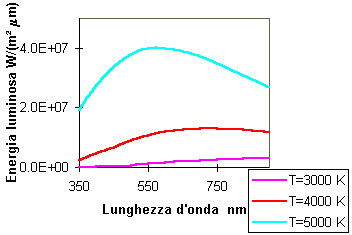
mostra la potenza irraggiata da un corpo nero in funzione della lunghezza
d'onda per diverse temperature; queste curve sono note come curve di distribuzione
spettrale. La grandezza W, in questa figura, è la potenza irraggiata
riferita all'unità di area e all'unità di lunghezza d'onda.
Essa è una funzione sia della lunghezza d'onda X sia della temperatura
T ed è chiamata funzione di distribuzione spettrale. Questa funzione,
W(X, T), ha un massimo a una lunghezza d'onda X. che è inversamente
proporzionale alla temperatura, secondo la legge dello spostamento di Wien
La funzione di distribuzione spettrale P(X, T) può essere calcolata
direttamente mediante la termodinamica classica, e il risultato può
essere confrontato con le curve sperimentali. Il risultato di questo calcolo
classico, noto come legge di Rayleigh-Jeans, è
P(ν, T) = 2π ck λ-4
Questo risultato è in accordo con i dati sperimentali nella regione
delle grandi lunghezze d'onda, ma è in forte disaccordo per piccole
lunghezze d'onda. Quando ν tende a zero, la P(ν, T) determinata sperimentalmente tende anch'essa a zero, mentre
la funzione calcolata diventa infinita poiché è direttamente
proporzionale a λ-4. Perciò,
secondo il calcolo classico, un corpo nero emette una quantità infinita
d'energia concentrata nelle lunghezze d'onda molto piccole. Questo risultato
era noto come catastrofe ultravioletta.
Nel 1900, il fisico tedesco Max Planck annunciò che, effettuando
una strana modifica nel calcolo classico, era in grado di dedurre una funzione
P(ν, T) che era in accordo con i dati sperimentali
per tutte le lunghezze d'onda. Planck trovò prima una funzione empirica
che fosse in accordo con i dati.
e poi cercò un modo per modificare il solito calcolo: egli trovò che riusciva a «dedurre» una funzione in accordo con i risultati sperimentali se faceva l'ipotesi inusitata che l'energia non fosse emessa o assorbita continuamente dal corpo nero, ma fosse invece emessa o assorbita in quantità discrete, o quanti. Il valore di un quanto di energia era direttamente proporzionale alla frequenza della radiazione E= h ν dove h è la costante di proporzionalità, nota oggi come «costante di Planck».
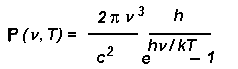
Il valore di h fu determinato da Planck adattando la sua funzione ai dati
sperimentali; il valore accettato oggi per questa costante è
h = 6,626 x 10-34 J . S = 4,136 x 10-15 eV s
Il risultato di Planck è mostrato nella figura assieme ai dati sperimentali.
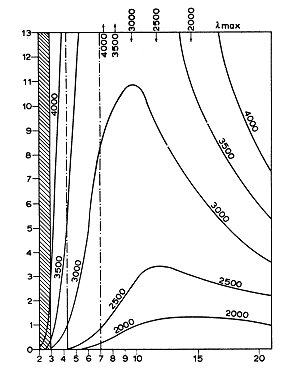
Sebbene Planck cercasse di trovare una giustificazione della costante h
nello schema della fisica classica, non ci riuscì. L'importanza fondamentale
della sua ipotesi di quantizzazione dell'energia, implicita nell'equazione
E = h ν non fu in generale compresa, finché
Einstein non applicò un'ipotesi simile per spiegare l'effetto fotoelettrico
e ipotizzò che la quantizzazione fosse una proprietà fondamentale
della radiazione elettromagnetica.