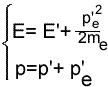 |
Consideriamo la luce costituita da particelle (fotoni) che interagiscono con un elettrone. Prima dell'urto il fotone ha una quantità di moto p= h / l . ed una energia E= h n . Considerando l'urto perfettamente elastico avremo che si conserverà sia l'energia che la quantità do moto del sistema. |
Si ha
|
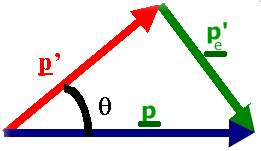 |
Il secondo termine dell'energia rappresenta l'energia cinetica dell'elettrone dopo l'urto. Applicando il teorema di Carnot al triangolo delle quantità di moto
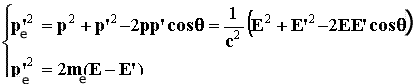
Ricordiamoci che per i fotoni :
| ν λ =c | P=h/λ | E=hν | e quindi: E = hc/λ | E= pc | P = E/c |
| allora uguagliando le due precedenti espressioni e dividendo per EE' si ottiene | 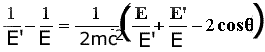 |
Sia e l’energia ceduta dalla radiazione elettromagnetica alla particella, sia cioè
| ε= E - E’ |
| allora si ha | 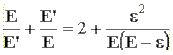 |
Supponiamo adesso (e sarà proprio questo il caso che ci interessa) che nell’interazione solo una piccola frazione dell’energia dell’onda elettromagnetica venga ceduta alla particella materiale, supponiamo cioè che risulti
| ε> << E |
| allora | 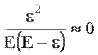 |
e così risulta |
a meno di infinitesimi del secondo ordine in e/E.
| Tanto per fare un esempio numerico se e/E fosse 1/10 (nel qual caso e non sarebbe poi così piccolo, rispetto ad E) allora e2/E(E - e) varrebbe 1/90 e sarebbe senz’altro trascurabile rispetto al numero 2. Se poi, più realisticamente, e/E fosse 1/100 allora l’espressione trascurata varrebbe solo 1/9900 |
| Si ha pertanto |