 In
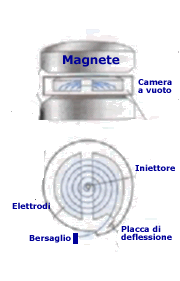
figura e' mostrato lo schema di un ciclotrone: esso consiste di una
cavità metallica cilindrica piatta divisa in due metà, che indicheremo
con D1 e D2, posta in un campo magnetico uniforme
B, parallello all'asse.
In
figura e' mostrato lo schema di un ciclotrone: esso consiste di una
cavità metallica cilindrica piatta divisa in due metà, che indicheremo
con D1 e D2, posta in un campo magnetico uniforme
B, parallello all'asse.
Le due cavità sono isolate e sono connesse ai poli di un generatore
che fornisce una tensione del tipo V=Vo cos(ωt),
detta radiofrequenza.
Quando lo ione percorre una delle cavità (Vcav=cost, Ecav=0)
non subisce alcuna forza elettrica, mentre invece viene accellerato
quando attraversa la regione tra le due D in cui c'è campo elettrico
variabile con legge sinusoidale (E=V/d).
Appena inserito nel ciclotrone, nella zona tra le due D, lo ione è
sottoposto alla forza elettrica e acquista energia cinetica:Ecinetica=qVx.
V è la differenza di tensione tra le due armature affacciate e coincidenti alle superfici piane delle due D. e x la distanza fra le due armature.
Entrando all'interno di una delle due D il campo B costringe lo ione a compiere una traiettoria circolare. Nel nostro caso operiamo tenendo presente che all'interno delle D la carica risulta essere sottoposta alla forza di Lorentz con F=qvB e per la geometria del sistema è uniforme e perpendicolare alla direzione di v e appartenente al piano su cui si muove la carica q.
Pertanto la particella carica si muove di moto circolare uniforme e possiamo scrivere:

e pertanto il tempo impiegato a percorrere mezza circonferenza risulta essere:

Detto tempo non dipende né dal raggio né dalla velocità iniziale e pertanto percorre sempre nello stesso intervallo temporale la semicirconferenza, fino a quando non varia la massa ossia finché un raggiungiamo velocità maggiori 1/2 c.
Dopo aver percorso una semicirconferenza all'interno di una D lo ione si riaffaccia all'intercapedine; se nello stesso tempo la radiofrequenza ha cambiato di segno lo ione subisce un'ulteriore accellerazione e il processo si ripete ad ogni semigiro fino a che viene raggiunta l'orbita di raggio massimo e la particella, con un'opportuno meccanismo, viene deflessa all'esterno del ciclotrone.
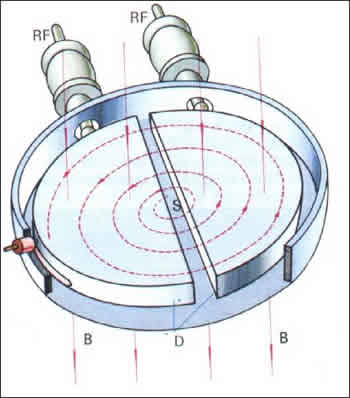
Analizziamo adesso quantitativamente il moto appena descritto. Se la particella α uscita dalla sorgente viene accellerata proprio dalla differenza di potenziale Vo, la velocità con cui essa entra per la prima volta in una delle D del ciclotrone è data da ½ mv12=qV; dopo un tempo
t1=½(2 πr1)/v1=πm/(qB)
lo ione esce da D1 per entrare in D2. Se nello stesso tempo la radiofrequenza ha cambiato di segno lo ione subisce una seconda accellerazione tra D1 e D2 e si ha
(1/2)mv22=½mv12+qV=2qV ossia l'energia cinetica dopo aver percorso 2 volte il campo elettrico è pari al doppio di quella acquisita dopo aver percorso il primo tratto tratto.
All'interno di D2 lo ione compie una semicirconferenza di raggio r2=(mv2)/(qB)>r1 nel tempo
t2=(1/2)(2πr2)/v2=πm/(qB)=t1
il tempo di percorrenza di un'orbita circolare in campo magnetico non dipende dalla velocità della particella.
Pertanto si ricava che il tempo impiegato per percorrere una semicirconferenza è costante mentre ad ogni giro la particella avrà acquisito una energia cinetica pari a 2qV.
La condizione di funzionamento è dunque che il tempo t impiegato a percorrere mezzo giro sia uguale al semiperiodo della radiofrequenza ovvero
TRF =(2π)/ωRF = qB/m
ωRF=qB/m=ω
la pulsazione della radiofrequenza deve essere uguale alla velocità angolare degli ioni. Il processo continua finchè lo ione raggiunge il raggio massimo R, determinato dalle dimensioni del magnete del ciclotrone. A tale raggio corrisponde la velocità massima dello ione,
vmax=qBR/m,
quindi l'energia cinetica massima è
Ecinetica,max=(1/2)mv2max=q2B2R2/(2m)
Dal momento che ad ogni giro lo ione acquista l'energia cinetica 2qV, il numero di giri per raggiungere l'energia cinetica massima è :
N=Ecinetica,max/2qV=qB2R2/(4mV)
a cui corrisponde il tempo
tN=2πmN/(qB)=πR2B/(2V).
A tal punto con un opportuno meccanismo il fascio di ioni accellerati viene deflesso all'esterno del ciclotrone e guidato verso la zone di utilizzazione e può avere inizio un nuovo ciclo di accellerazione; si dice che il ciclotrone è una macchina a funzionamento pulsato, cioè non continuo. Anche questo metodo presenta una limitazione fondamentale. Al crescere della velocità delle particelle la loro massa cambia e cambia di consegnuenza la loro velocità angolare( ω); più comunemente ci si riferisce alla frequenza di rivoluzione che deve essere scritta
ν=qB/(2πm)
All'aumentare di v la frequenza ν diminuisce e si perde il sincronismo con la radiofrequenza che ha la frequenza fissa νRF=νo ; dove νo è la cosiddetta frequenza di ciclotrone che si riferisce alla massa a riposo ovvero a piccole velocità. Lo ione non risente più della stessa d.d.p. accelleratrice e finisce per presentarsi nell'intercapedine tra le due D in istanti in cui la d.d.p. è di segno sbagliato, venendo decelerato.
Il valore massimo di energia cinetica raggiungibile dagli ioni risulta dell'ordine di qualche decina di MeV. Risulta inoltre che il metodo è inapplicabile agli elettroni i quali, avendo massa molto inferiore a quella deglio ioni, raggiungono molto presto velocità relativistiche e subiscono notevoli variazioni di massa.
La difficoltà descritta e' stata parzialmente superata agendo su νRF che viene opportunamente diminuita durante il processo di accellerazione in modo da seguire la variazione della frequenza di rivoluzione; a questo punto però il limite viene posto dalle dimensioni del magnete, in quanto al crescere dell'energia deve crescere R. Il più grande ciclotrone a frequenza variabile, detto sincrociclotrone, ha raggiunto energie di circa 600 MeV con fasci di protoni.
Per ottenere energie superiori è stato inventato un diverso sistema magnetico, utilizzato sempre in combinazione con il principio dell'orbita circolare che consente di riapplicare la d.d.p. acceleratrice; la macchina è denominata sincrotrone e la realizzazione maggiore attualmente funzionante permette di ottenere protoni con energia di 1TeV.