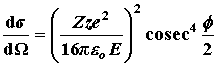Modello interpretativo
Come spiegare quanto osservato, utilizzando un modello in grado non solo
di giustificare quanto osservato ma in grado di prevedere una corretta interpretazione
della struttura interna del target e quindi, nel caso in esame, dell’atomo.
STRUTTURA DELL’ESPERIMENTO
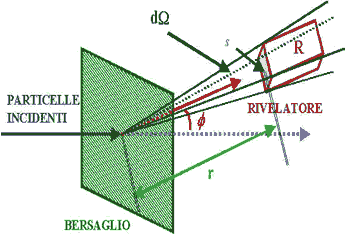
Come già accennato, gli esperimenti di scattering sono caratterizzati
dalla presenza di un rivelatore di sezione S
posto perpendicolarmente alla direzione del fascio di particelle incidenti
e ad una distanza r dal target
(il rivelatore analizza solo le particelle incidenti solo nella sezione
S).
Il numero r delle particelle rilevate è
calcolabile attraverso la seguente formula:
n è il numero di centri diffusori (e cioè i punti in cui
il fascio di particelle può essere deflesso, ovvero i punti in cui
può avvenire un urto) per unità di volume ed h è lo
spessore della lamina.
Negli esperimenti n, h, S, r
sono mantenuti costanti, cosicché F, l’angolo
di deflessione, sarà legato in qualche modo al rapporto ds/dW
che chiameremo sezione d'urto differenziale.
Sezione d'urto
|
Per capire il concetto di sezione d’urto
è possibile rifarsi ad un esperimento che coinvolga dei palloncini
e dei proiettili sparati contro di essi (interazione palloncino-proiettile).
Dalla figura si può notare che la probabilità di colpire
un palloncino dipende da tre fattori:
- n numero di
palloncini per unità di volume [pertanto il numero
di palloncini che occupano il volume preso in considerazione
N= nV = n Sh]
- Dallo spessore h
dello strato da essi occupato ;
- Dalla superficie, o sezione (sT),
che i palloncini presentano nella direzione dei proiettili.
C’è quindi una relazione tra la densità
dei palloncini, lo spessore da essi occupato e la sezione che
i palloncini rivolgono verso i proiettili in arrivo, che esprime
la probabilità di un contatto tra palloncini e proiettili,
attraverso la seguente formula:
|
 |
Da questo semplice esempio è possibile generalizzare la formula,
che ha validità per qualunque esperimento di scattering.
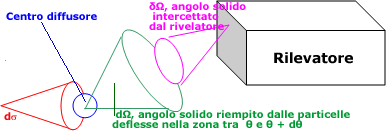
Consideriamo un esperimento qualsiasi in cui un fascio di radiazioni
o particelle si muovono in un cono di sezione ds
(sezione del cono in corrispondenza del centro diffusore. Detto fascio
viene diffuso in tutte le direzioni anche se noi nel caso in esame
consoderiamo solo l'angolo solido dW compreso
tra T e T+ dT
e le radiazioni o le particelle vengono rilevate solo se entrano nell'angolo
solido dW che il rilevatore è in
grado di intercettare.
Cerchiamo ora di comprendere più nello specifico cosa si
intende per sezione d’urto differenziale.
definizione di angolo solido:è una grandezza
geometrica tridimensionale.
Consideriamo una sfera trasparente di
raggio r = 1 m. con al centro C una sorgente luminosa puntiforme che
illumina la zona S = 1 m2.
Si definisce angolo solido dw lo spazio
racchiuso nel cono di luce di base S e di vertice C; l' unità
di misura è lo steradiante, ovvero dw=S/
r2
Come nel caso dei palloncini, la probabilità che una particella
venga osservata dal rivelatore, è direttamente proporzionale
al numero n dei centri
diffusori, allo spessore h da essi occupato, dipende dal rapporto
fra i due angoli solidi T e
T+ dT ed il coefficiente di proporzionalità
è costituito dalla zona di deflessione dW.
La formula della proporzionalità risulta quindi essere:
Qui si evidenzia il rapporto o sezione d’urto differenziale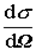 ,
costituita quindi dal rapporto fra la zona di deflessione determinata
dal centro diffusore e la zona riempita dalle particelle deflesse. ,
costituita quindi dal rapporto fra la zona di deflessione determinata
dal centro diffusore e la zona riempita dalle particelle deflesse.
Se noi riscriviamo l’angolo solido dW come
rapporto fra la superficie S del rivelatore ed il quadrato della distanza
r2, visto che è così calcolabile, e poi sostituiamo
questa scrittura nella precedente formula della probabilità,
otteniamo nuovamente la scrittura già trovata nell’esempio
dei “palloncini”.
|
Il modello di RUTHERFORD
|
Per spiegare i dati sperimentali ricavati
da Geiger e Marsden, Rutherford ipotizzò un modello per gli atomi
del target che attribuisse loro certe caratteristiche:
- Come abbiamo visto, grandi angoli di deflessione dovevano dipendere
da un singolo urto
- Possiamo pensare all’atomo come formato da un nucleo puntiforme
di carica Ze il quale possiede tutta la massa dell’atomo stesso
e da una zona attorno ad esso di carica Ze- pressoché vuota (ciò
è spiegabile con il fatto che la maggior parte delle particelle
? proseguono indisturbate)
- Dopo l’urto il nucleo resta pressoché indisturbato,
essendo immobile e non acquistando energia
- L’unica forza che consideriamo nell’esperimento è
quella elettrostatica (perché le particelle ? sono cariche positivamente
e di conseguenza devono essere deflesse da cariche elettriche)
- Se la deflessione non è troppo piccola l’interazione
si considera avvenire con il solo nucleo, e non con il campo che lo
attornia
- L’interazione non è descritta attraverso la relatività,
in quanto le energie in gioco non sono sufficientemente alte (ovvero
l’energia con cui sono lanciate, circa 10 MeV è molto minore
alla loro massa espressa in eV, che risulta essere di circa 4 GeV)
- L’interazione è spiegata secondo la meccanica classica,
poiché la meccanica quantistica non era ancora stata sviluppata
Così Rutherford riuscì a scrivere la formula per la sezione
d’urto differenziale con Ze come carica del nucleo bersaglio e ze
la carica della particella α:
Questa formula è il risultato finale del procedimento matematico
volto a trovare il legame fra l’Ec della particella incidente,
l’angolo di deflessione Φ ed il parametro
d’urto b (cioè la distanza fra la traiettoria della particella
ed il nucleo, da cui dipende l’interazione, intesa come differente
deflessione).
Dalla formula così ricavata, possiamo notare che la sezione d’urto
differenziale è proporzionale alla cosec4Φ/2.
Ciò significa che se l’angolo di deflessione è zero,
la sezione d’urto assume valore di infinito: ciò implicherebbe
il verificarsi di una deviazione delle particelle incidenti in ogni caso,
ovvero con una distanza qualsiasi fra le traiettorie delle particelle
incidenti e la posizione del nucleo (parametro d’urto). Questo perché
è stata trascurata la carica negativa degli elettroni.
Inoltre la sezione d’urto diminuisce molto se aumenta l’angolo
Ψ, di conseguenza molte delle particelle proseguiranno
indisturbate.
Come si può notare dalla formula, la sezione d’urto è
direttamente proporzionale alla carica delle particelle inviate ed a quella
del nucleo ed inversamente proporzionale al quadrato dell’energia
cinetica delle particelle incidenti. Poiché la carica viene elevata
al quadrato, la deflessione è indipendente dal segno di essa e
quindi in esperimenti di questo tipo non ci è possibile dire se
avviene un’attrazione o una repulsione e dal momento che l’energia
è al denominatore, più energetiche saranno le particelle
inviate, meno saranno deflesse.
|