1° PROBLEMA RISOLTO
In un cerchio di raggio R è data una corda AB =R 
3.
Determinare un'altra corda AC in modo che sia AC2 - BC2
= 3 R2.
Premessa: non essendo stato precisato su quale arco porre C si devono risolvere due problemi.
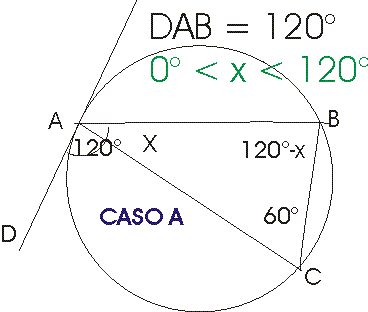
- caso A : C appartiene al maggiore degli archi AB
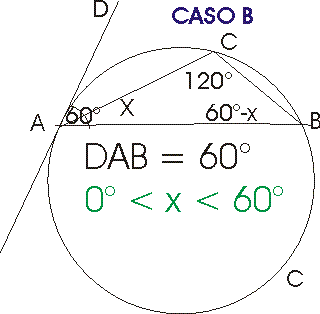
- caso B: C appartiene all'altro arco.
Proprietà generali:
-
se AB= r 3 allora l'angolo ACB
- nel caso A vale 60°
- nel caso B vale 120°
-
Posto BAC = x detto angolo è interno
all'angolo DAB e quindi
- nel caso A 0°x<120°
- nel caso B 0°<x<60°
- Problema da risolvere sempre col teorema della corda.
 |
 |
CASO B
 |
 |