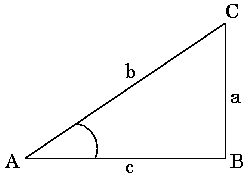Problemi sui triangoli rettangoli

Christopher Kent Mineman - Didattica in rete

TEORIA IN PILLOLE

 

UN TRIANGOLO RETTANGOLO 

 

Partendo dalla definizione di seno si ricava: 

CATETO = IPOTENUSA PER IL SENO DELL'ANGOLO ACUTO AD ESSO OPPOSTO

ossia a = b sen α

Partendo dalla definizione di coseno si ricava: 

CATETO = IPOTENUSA PER IL SENO DELL'ANGOLO ACUTO AD ESSO ADIACENTE

ossia a = b cos β

 

Partendo dalla definizione di coseno si ricava: 

CATETO1 = CATETO2 PER LA TANGENTE DELL'ANGOLO ACUTO AD ESSO OPPOSTO

ossia a = b tang α

 

IMPOSTAZIONE DEI PROBLEMI

Dalla geometria euclidea si ricava che un triangolo rettangolo è risolvibile quando di esso conosciamo la misura di due elementi dei quali almeno uno è la misura di un lato.

RISOLVERE UN TRIANGOLO VUOL DIRE DETERMINARE DELLO STESSO LA MISURA DEI TRE LATI E DEI TRE ANGOLI INTERNI.

Ricordarsi che L'ipotenusa è maggiore di ogni cateto.

La somma degli angoli acuti vale sempre 90°.

Un angolo acuto misura 90° - l'ampiezza dell'altro angolo acuto.

β = 90° - γ (β e γ angoli acuti e complementari)

Considereremo sempre 

  • b l'ipotenusa

  • a (α l'angolo acuto ad esso opposto)  cateto  

  • c (γ l'angolo acuto ad esso opposto)  cateto

PROBLEMI TIPO  

CON CALCOLATRICE

Conosciamo b=33,45  e γ = 53°45'25''

RISOLUZIONE:

  • α = 90°-53°45'25'' = 36°14'15'' = 36,2375 ( decimalizzato)[36+14/60+15/3600]

  • a = b tang α= 33,45 tang 36,2375 = 24,51 (troncare non approssimare).

  • c = b/ sen γ = 33,45 / sen 53°45'25'' = 33,45 / sen 53,7625 = 41,47

SENZA CALCOLATRICE

Di un triangolo rettangolo si conosce il sen α = 3/5 e si sa che la differenza fra l'ipotenusa e il cateto opposto all'angolo β è 2 cm. Determinare perimetro e area.

RISOLUZIONE

  • In questo problema a e b sono i cateti e l'ipotenusa misura c.

  • c - b = 2

  • Da sen α = 3/5 si ricava immediatamente dalla relazione fondamentale cos α = 4/5

  • Essendo β l'angolo complementare ad α avremo : cos β=3/5 e sen β = 4/5 (pertanto conosciamo gli angoli).

  • b=c sen β e quindi b = 4/5 c

  • Tornando alla condizione iniziale c-b=2 avremo c -4/5 c = 2 ossia c/5 = 2

  • c= 10 cm

  • b=4/5 10 = 8 cm

  • a = c sen α = 10 3/5 = 6 cm

  • Perimetro= (10 + 8 + 6) cm = 24 cm

  • Area = 6 * 8 /2 cm2 = 24 cm2

PROBLEMI PROPOSTI

CON USO DELLA CALCOLATRICE

UN TRIANGOLO RETTANGOLO

1° a=26,48 b=52,54
2° a=56,6 c=33,4
3° α=36°45' b=55
4° γ=55°45'24'' c=33,33
5° a=56,4 b=52,5
6° α=56°,6543 c=33,4
7° α=16°45' c=55,333
8° α=15°37'24'' b=33,33
9° a=1,03 b=1123,4
10° α= 33°45'24'' β=90°


SENZA CALCOLATRICE.

1° Determinare l'ipotenusa di un triangolo rettangolo sapendo che, detto a uno degli angoli acuti, è sen α = 5/13 e che la differenza delle proiezioni dei due cateti  sull'ipotenusa è 238 cm.
2° Un cateto di un triangolo rettangolo è 50 cm e la sua proiezione sull'ipotenusa è 14 cm. Determinare la tangente dell'angolo opposto al cateto noto e il perimetro dei triangolo.
3° Nel triangolo isoscele ABC, la base AB è lunga 28 cm e l'altezza CH 48 cm. Determinare il coseno dell'angolo ABC, il seno dell'angolo ACB e l'altezza AK relativa al lato BC.
4° Determinare la misura del perimetro e dell'area di un trapezio rettangolo ABCD sapendo che l'angolo ABC è di 60° e che la diagonale minore AC è perpendicolare al lato obliquo BC = 12 cm
5° Calcolare gli angoli di un triangolo rettangolo sapendo che un cateto è cm (3 - 1) e l'area è 1 cm2