Risoluzione problemi
senza calcolatrice
RISOLVERE I SEGUENTI PROBLEMI
| 1° |
Determinare l'ipotenusa
di un triangolo rettangolo sapendo che, detto a uno degli angoli
acuti, è sen α =
5/13 e che la differenza delle proiezioni dei due cateti
sull'ipotenusa è 238 cm. |
| 2° |
Un cateto di un triangolo rettangolo è 50 cm e
la sua proiezione sull'ipotenusa è 14 cm. Determinare la
tangente dell'angolo opposto al cateto noto e il perimetro dei
triangolo. |
| 3° |
Nel triangolo isoscele ABC, la base AB è
lunga 28 cm e l'altezza CH 48 cm. Determinare il coseno dell'angolo
ABC, il seno dell'angolo ACB e l'altezza AK relativa al lato BC. |
| 4° |
Determinare la misura del perimetro e dell'area
di un trapezio rettangolo ABCD sapendo che l'angolo ABC è di 60°
e che la diagonale minore AC è perpendicolare al lato obliquo
BC = 12 cm |
| 5° |
Calcolare gli angoli di un triangolo rettangolo
sapendo che un cateto è cm ( 3
- 1) e l'area è 1 cm2 |
Risoluzione problemi proposti
|
1° problema
 |
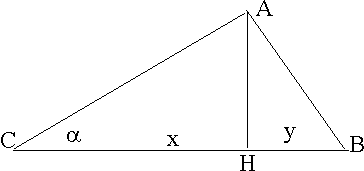| 2 condizioni - 2
incognite.
Scegliere per incognite CH = x e HB = y
Se x-y = 238 allora x = y+238 e l'ipotenusa CB=
2y+238.
Se senα = 5/13 allora cos
α = 12/13.
Nel triangolo ACH l'ipotenusa AC
= CH / cos α = 13(238+x)/12
Dalla definizione di coseno cos α
= CA / CB e quindi:
12/13 =
[13(238+x)]/[12(2y+238)]
144(2y+238)=169(238+y)
288y +
144*238 = 169*238 + 169 y
119y =
238*(169-144)
y = 50
Ipotenusa 338
cm |
2° problema
|
| Dati: AB= 50 - HB =
14
Richiesta: calcolare la tangente di α
α = 90° -
Tang α = tang (90° -β)
= cotang β .
tang β = AH/HB - cotang β=
HB / AH
tang α = HB / AH = 14/48 =
7 / 24
Con Pitagora si determina la lunghezza di AH = 48 |
3° problema
|
|
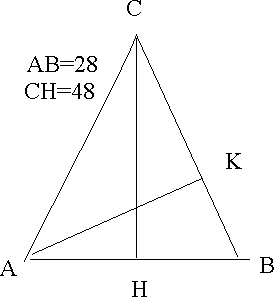
| Con Pitagora si determina la lunghezza di CB=CA=
50
HB = 14
cos ABC = HB / CB = 14/50 = 7 / 25
sen ABC = 24/25 ( relazione fondamentale)
sen ACB = sen ( 180 - 2 ABC) = sen 2 ABC da cui
sen ACB = 2 sen ABC cos ABC = 336/625
AK = AB sen ABC = 28 *24 / 25 = 672/25 |
4° problema
 |
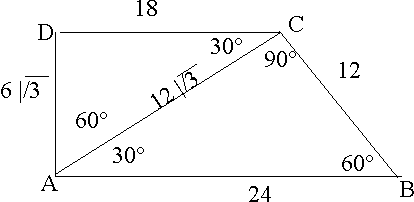Si risolve utilizzando le proprietà
dei triangoli rettangoli metà di triangoli
equilateri.
- La misura del cateto opposto all'ipotenusa = 1/2
ipotenusa
- cateto opposto all'angolo di 60° = ipotenusa 3
/2
Abbiamo due triangoli rettangoli su
cui applicare queste proprietà.
La risoluzione è sulla figura. |
5° problema
|
| AB = 3
- 1
AB * AC = 2 ( area * 2)
AC = 2/( 3
-1) razionalizzando si ottiene
AC= 3
+ 1
tang α = AB
/ AC = ( 3
-1)/(3 +1)
razionalizzando si ottiene:
2 - 3
α =
15° - β =
75°
|
|