 GLI ANGOLI
GLI ANGOLI
Angolo è ciascuna delle due parti nelle quali un piano viene diviso da due semirette aventi la stessa origine. Le due semirette sono dette lati dei due angoli e l'origine comune il loro vertice.
Data una circonferenza avente il centro nel vertice di un angolo, si chiama arco circolare (o più semplicementearco quella parte di circonferenza, interna all'angolo, avente per estremi i punti di intersezione con i lati dell'angolo stesso.
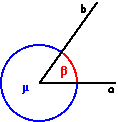 |
Ciascun angolo è orientato se definiti i lati si determina il verso di percorrenza dal primo lato al secondo. ordinando i suoi due lati in uno dei due modi possibili ("a, b" oppure "b, a"), convenzionalmente si pone come verso positivo di percorrenza quello antiorario (nel caso della figura a sinistra il senso positivo è da "a" a "b"). |
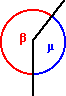
La parte non contenente i prolungamenti dei lati si dice ANGOLO
CONVESSO, l'altro ANGOLO CONCAVO (nel disegno sopra riportato
l'angolo convesso è β
mentre μ è concavo).
Vediamo ora alcuni angoli particolari:
 ANGOLO
RETTO ( β
= 90°
) ANGOLO
RETTO ( β
= 90°
) |
 ANGOLO
ACUTO (β
<90°
) ANGOLO
ACUTO (β
<90°
) |
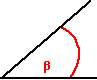
| ANGOLO OTTUSO ( β > 90° ) |
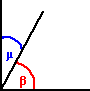 ANGOLI
COMPLEMENTARI (β
+ μ= 90°
) ANGOLI
COMPLEMENTARI (β
+ μ= 90°
) |
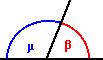 ANGOLI
SUPPLEMENTARI (β+μ=180°
) ANGOLI
SUPPLEMENTARI (β+μ=180°
) |
 ANGOLI
ESPLEMENTARI ( β+μ =360°) ANGOLI
ESPLEMENTARI ( β+μ =360°) |
- Seno e coseno sono funzioni periodiche con periodo 2π :sen(x+360°)=sinx - cos(x+360°)=cosx.
Quindi esprimendo l'angolo in radianti
sen(x+2π)=sinx - cos(x+2π)=cosx.
I valori del seno e del coseno sono uguali per gli angoli complementari:
cos x=sen(π/2-x)
senx=cos(π/2-x)
- Le funzioni goniometriche sono legate dalla relazione fondamentale:
sen2 x + cos2 x=1.
- Il seno è una funzione dispari ossia sen(-x) = sen x. Il coseno è una funzione pari ossia cos(-x)=cosx. Di conseguenza i loro diagrammi sono :
- seno: simmetrico rispetto all'origine e quindi per la sua periodicità simmetrico rispetto al punto (π, 0)
- Coseno: simmetrico rispetto alla retta x=0 e quindi per la periodicità anche rispetto alla retta x= π
- Il seno e il coseno sono funzioni limitate tra -1 e 1.
DIAGRAMMA DELLA FUNZIONE Y=sen X
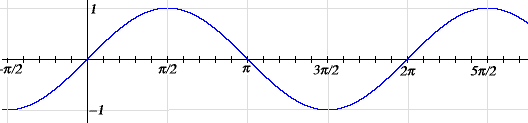
Il seno è definito in R e essendo periodica si ripresenta identicamente dopo un periodo. Quanto visto vale anche per la funzione coseno
DIAGRAMMA DELLA FUNZIONE Y=cos X
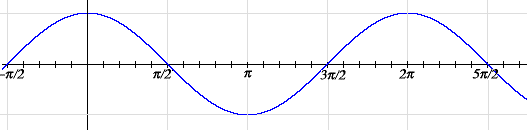
DIAGRAMMA DELLA FUNZIONE Y=tang X
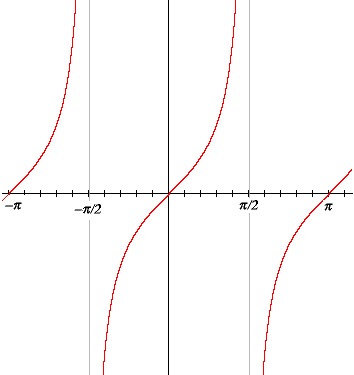
DIAGRAMMA DELLA FUNZIONE Y=cotg X
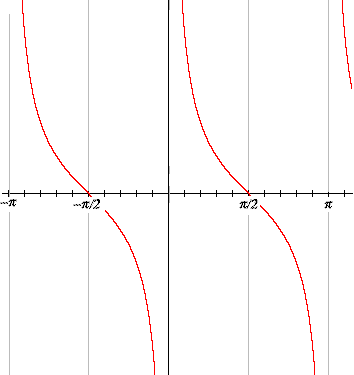
DIAGRAMMA DELLA FUNZIONE Y=sec X
La secante essendo il reciproco della funzione coseno assumerà solo valori maggiori di 1 o minori di -1.Se il coseno vale 0 la cosecante non esiste ossia la funzione presenta in corrispondenza di tali angoli un asintoto verticale