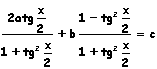|
RIDUCIBILI AD EQUAZIONI IN UNA VARIABILE |
REGOLE DI VALIDITA' GENERALE: Ridurre tutto in un'equazione in seno e coseno; eliminare tangenti, cotangenti, secanti e cosecanti con le opportune trasformazioni. fatti i calcoli e le semplificazioni ridurre tutto in un'equazione o in seno o in coseno. Risolvere nella variabile residua. |
||||
|
Equazioni omogenee di 1° grado |
equazioni del tipo: a sen x + b cos x=0. Dividere ogni termine per cos x e si ottiene un'equazione in tangente a tang x + b = 0 | ||||
|
Equazioni omogenee di 2° grado |
equazioni del tipo a sen2 x + b sen x cos x + c cos2x = 0. Dividere per cos2x ottenendo un'equazione del tipo a tang2 x + b tang x + c = 0 equazioni del tipo a sen2 x + b sen x cos x + c cos2x + d = 0. Prima di dividere moltiplicare il termine d per sen2 x + cos2 x ottenendo: (a+d) sen2 x + b sen x cos x + (c+d) cos2x = 0 Dividere per cos2x ottenendo un'equazione del tipo (a+d) tang2 x + b tang x + (c+d) = 0 |
||||
| Equazioni lineari |
Sono equazioni del tipo a sen x + b cos x = c , con a, b, c numeri
reali assegnati, che supporremo diversi da zero (infatti nel caso in cui
a o b fossero uguali a zero si avrebbe di nuovo un'equazione elementare,
il caso in cui c sia uguale a zero verrà esaminato più avanti).Per
risolvere questo tipo di equazioni conviene sostituire sen x e cos x con
le loro corrispondenti espressioni razionali in funzione di tg(x/2) valide
perx
svolgendo i calcoli si otterrà l'equazione di secondo grado in tg(x/2):
se questa avrà due soluzioni reali, le chiameremo r1 e r2 , si avranno le seguenti equazioni elementari, di cui si conosce la soluzione:
Per l'equazione lineare data potrebbero essere però soluzioni anche i valori del tipo x = π + 2kπ, che non si possono avere col metodo descritto a causa delle restrizioni imposte dalle formule usate; se però si verifica il caso in cui b + c = 0 , si ha anche soluzioni per x = π + 2kπ. |