TEORIA IN PILLOLE
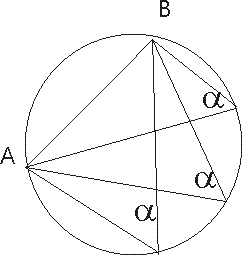
TEOREMA DELLA CORDA
|
|
Una corda è sempre uguale al diametro per il seno dell'angolo alla circonferenza
| AB= 2R sen α |
Non occorre avere un triangolo, tanto meno il triangolo rettangolo avente per ipotenusa il diametro!
![]()
TEOREMA DEI SENI
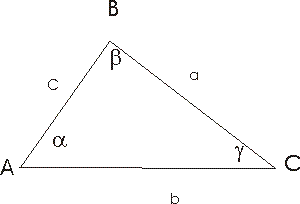 |
Dato un triangolo qualsiasi valgono sempre le seguenti
relazioni:
|
![]()
Si può utilizzare il teorema dei seni se si conosce la misura DI TRE ELEMENTI (2 ANGOLI E UN LATO - 2 LATI ED UN ANGOLO)
Non si può utilizzare il teorema dei seni
solo nei seguenti due casi:
In questi casi si deve utilizzare il teorema di Carnot. |
![]()
 3-1)
3-1)