- sec α = 1/cosα
- cosecα=1/senα
- tangα= senα/cosα
- cotangα=cosα/senα
Effettuare i calcoli e le semplificazioni.
Infine cercare di rendere l'espressione dipendente da una sola variabile trigonometrica
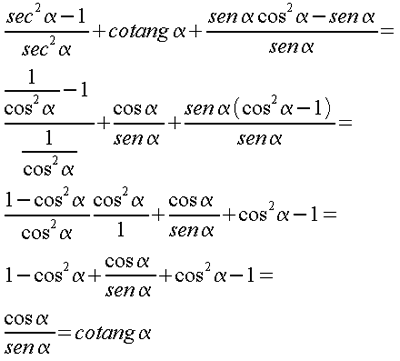
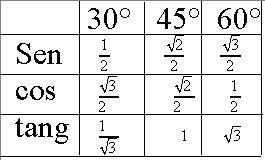
ANGOLI NOTEVOLI
Seno crescente - Coseno decrescente ( denominatore sempre 2) Per gli angoli 0° - 90° - 180° - 270° - 360° far riferimento ai valori limite sulla circonferenza goniometrica |
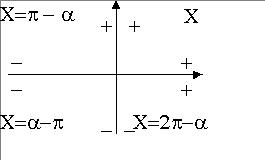
ANGOLI ASSOCIATIOsservare la seguente tabella. è l'angolo argomento di una funzione trigonometrica di cui ci chiedono il valore X è l'angolo associato appartenente al primo quadrante. L'asse delle ordinate ci permette di ricavare il segno del seno nei vari quadranti. L'asse delle ascissa il segno del coseno. Determinato il segno il valore della funzione è quello della funzione dell'angolo associato riferito al primo quadrante.
ESEMPIO: sen (210°)= sen (180° + 30°) = Angolo del terzo quadrante - ordinata negativa - seno associato quello dell'angolo 30° - sen 30° = -1/2 |
IDENTITA'Risolvere separatamente ogni espressione ( a sinistra e a destra del segno di = ) e operare in modo da ottenere 2 identità. ( NON E' LECITO SPOSTARE TERMINI DA UNA PARTE ALL'ALTRA DEL SEGNO DI UGUALE, SE NON SI ESPLICITA LA PROPRIETA' CHE SI STA SFRUTTANDO). Per i calcoli far riferimento alla risoluzione di espressioni. |
FORMULE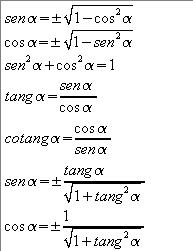
|
EQUAZIONI ELEMENTARI
X= α + 2Kπ ESEMPIO sen X = - 1/2 Seno negativo nel 3° e 4° quadrante - sen x = 1/2 se x= π/6 , pertanto a1= π+π/6 = 7/6π a2=2π-π/6=11/6π x1= 7/6 π + 2Kπ x2= 11/6π +2Kπ |