Equazioni di vari tipi

Christopher Kent Mineman - Didattica in rete

Problemi
Detto P un punto della semicirconferenza di diametro AB=2r, condurre la retta t bisettrice dell'angolo PAB e indicare con C e D i punti di intersezione della retta t rispettivamente con la circonferenza e la retta parallela per B alla retta AP.

Detto PAB= 2x si determini :

  1. Le ampiezze degli angoli dei triangoli APC e ADB.
  2. Le lunghezze dei lati dei due triangoli.
  3. il valore dell'angolo per cui PC + AD =3r 2

SOLUZIONE

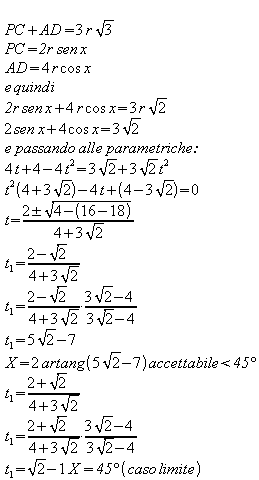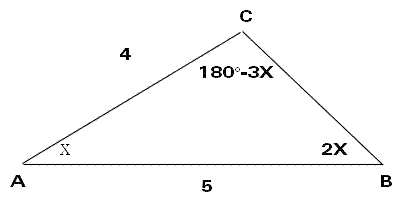
Dai dati si ricava che il triangolo ABD è isoscele con base AD ( essendo l'angolo in D uguale all'angolo PAD - alterni interni ) quindi BD = AB = 2 r. Essendo CB perpendicolare ad AD è altezza, mediana e bisettrice e pertanto AC = 2r cos x e AD= 4 r cos x.

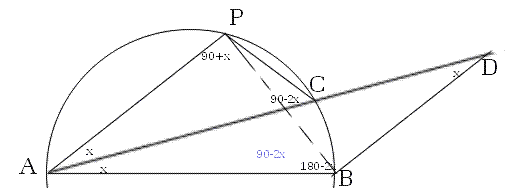
Nel triangolo APC, l'angolo in C insistendo sulla stessa corda dell'angolo alla circonferenza ABP ha la stessa ampiezza dello stesso quindi PCA = 90°- 2x e per differenza l'angolo APC = 180°- x - (90° - 2x) = 90° + x.

Utilizzando il teorema della corda

  • PC = 2r sen x
  • AC = 2r sen ( 90° + x) = 2r cos x
  • AP = 2r sen ( 90°- 2x) = 2r cos 2x

Per il terzo punto si ottiene

 

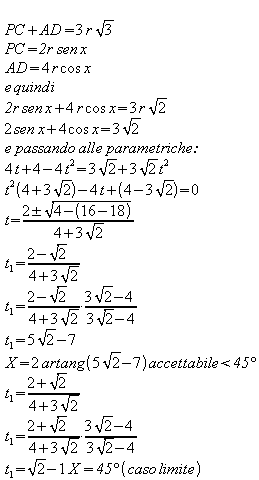
PROBLEMA N 2

Del triangolo ABC si sa che BC = 4 cm, AB = 5 cm, e che l'angolo ABC = 2 BAC . Determinare l'area e il perimetro del triangolo.

Per determinare l'ampiezza dell'angolo X utilizziamo il teorema dei seni sui lati AB e AC e quindi